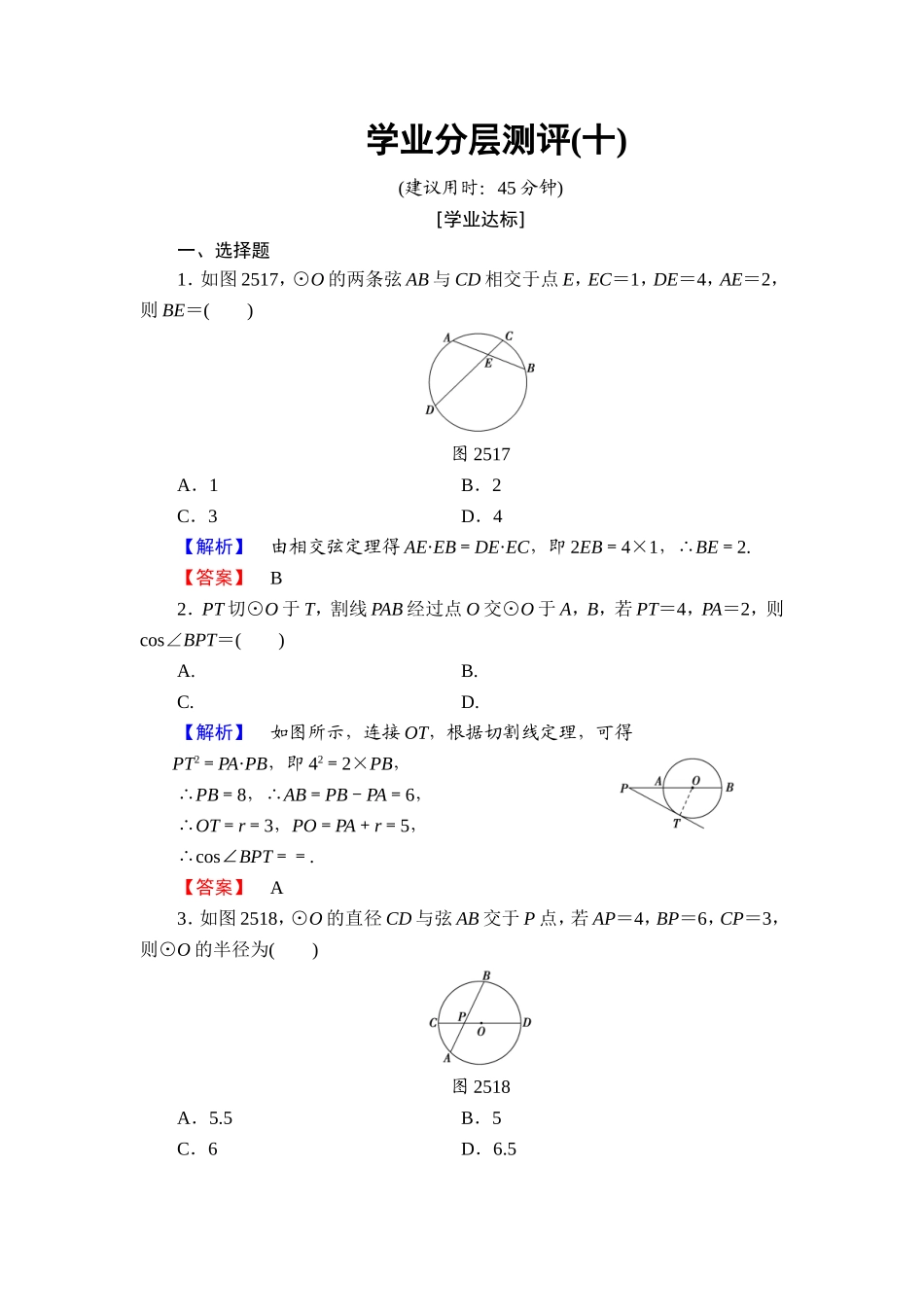
学业分层测评(十)(建议用时:45分钟)[学业达标]一、选择题1.如图2517,⊙O的两条弦AB与CD相交于点E,EC=1,DE=4,AE=2,则BE=()图2517A.1B.2C.3D.4【解析】由相交弦定理得AE·EB=DE·EC,即2EB=4×1,∴BE=2.【答案】B2.PT切⊙O于T,割线PAB经过点O交⊙O于A,B,若PT=4,PA=2,则cos∠BPT=()A.B.C.D.【解析】如图所示,连接OT,根据切割线定理,可得PT2=PA·PB,即42=2×PB,∴PB=8,∴AB=PB-PA=6,∴OT=r=3,PO=PA+r=5,∴cos∠BPT==.【答案】A3.如图2518,⊙O的直径CD与弦AB交于P点,若AP=4,BP=6,CP=3,则⊙O的半径为()图2518A.5.5B.5C.6D.6.5【解析】由相交弦定理知AP·BP=CP·PD, AP=4,BP=6,CP=3,∴PD===8,∴CD=3+8=11,∴⊙O的半径为5.5.【答案】A4.如图2519,在Rt△ABC中,∠C=90°,AC=4,BC=3.以BC上一点O为圆心作⊙O与AC,AB都相切,又⊙O与BC的另一个交点为D,则线段BD的长为()【导学号:07370047】图2519A.1B.C.D.【解析】观察图形,AC与⊙O切于点C,AB与⊙O切于点E,则AB==5.如图,连接OE,由切线长定理得AE=AC=4,故BE=AB-AE=5-4=1.根据切割线定理得BD·BC=BE2,即3BD=1,故BD=.【答案】C5.如图2520,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.给出下列三个结论:图2520①AD+AE=AB+BC+AC;②AF·AG=AD·AE;③△AFB∽△ADG.其中正确结论的序号是()A.①②B.②③C.①③D.①②③【解析】①项, BD=BF,CE=CF,∴AD+AE=AC+CE+AB+BD=AC+AB+CF+BF=AC+AB+BC,故①正确;②项, AD=AE,AD2=AF·AG,∴AF·AG=AD·AE,故②正确;③项,延长AD于M,连接FD, AD与圆O切于点D,则∠GDM=∠GFD,∴∠ADG=∠AFD≠∠AFB,则△AFB与△ADG不相似,故③错误,故选A.【答案】A二、填空题6.如图2521,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线交于D,过点C作BD的平行线与圆交于点E,与AB交于点F,AF=3,FB=1,EF=,则CD=________.图2521【解析】因为AF·BF=EF·CF,解得CF=2,由CE∥BD,得=,所以=,即BD=.设CD=x,AD=4x,所以4x2=,所以x=.【答案】7.如图2522,AB为圆O的直径,PA为圆O的切线,PB与圆O相交于D,若PA=3,PD∶DB=9∶16,则PD=________,AB=________.图2522【解析】由于PD∶DB=9∶16,设PD=9a,则DB=16a.根据切割线定理有PA2=PD·PB.又PA=3,PB=25a,∴9=9a·25a,∴a=,...