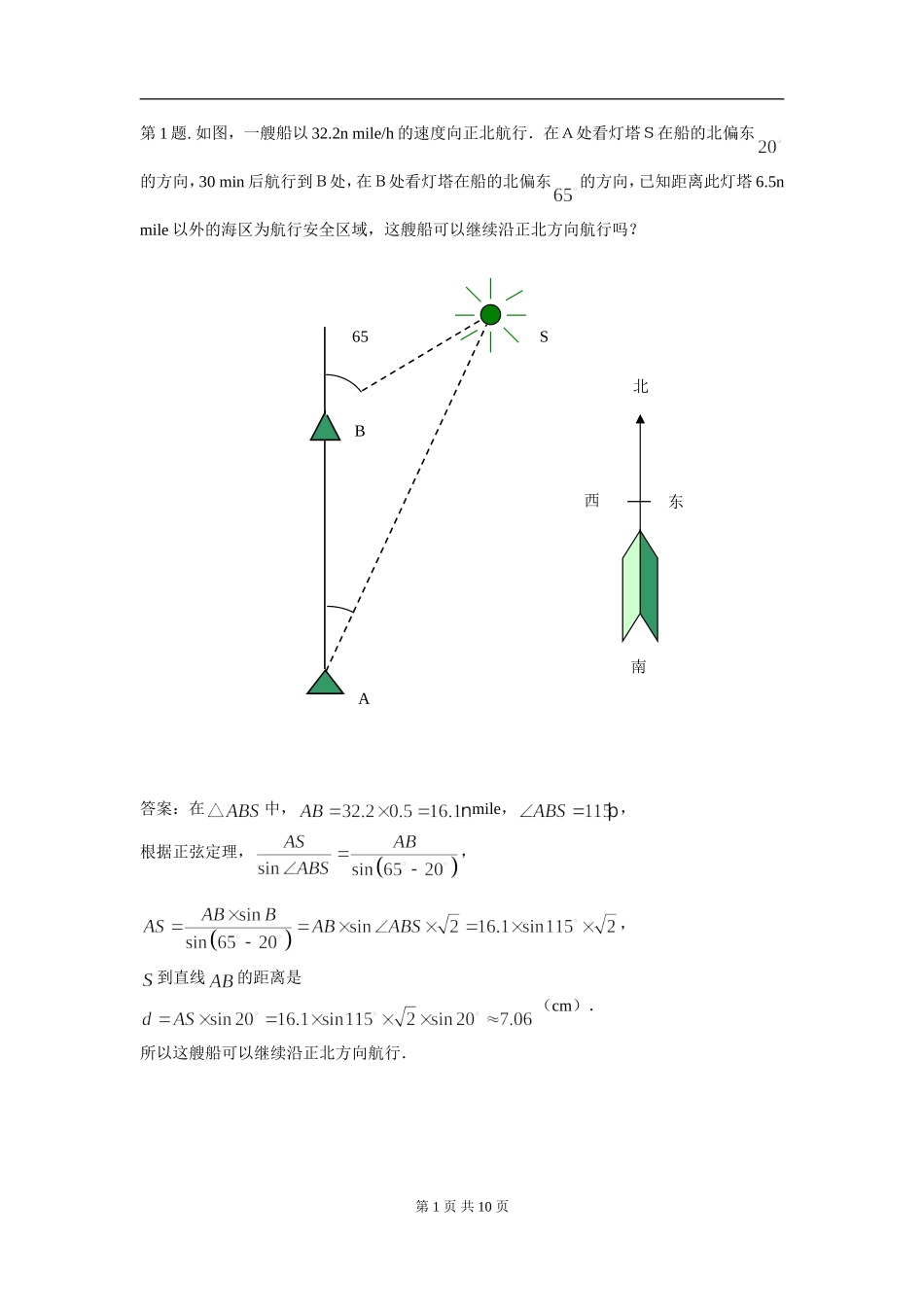
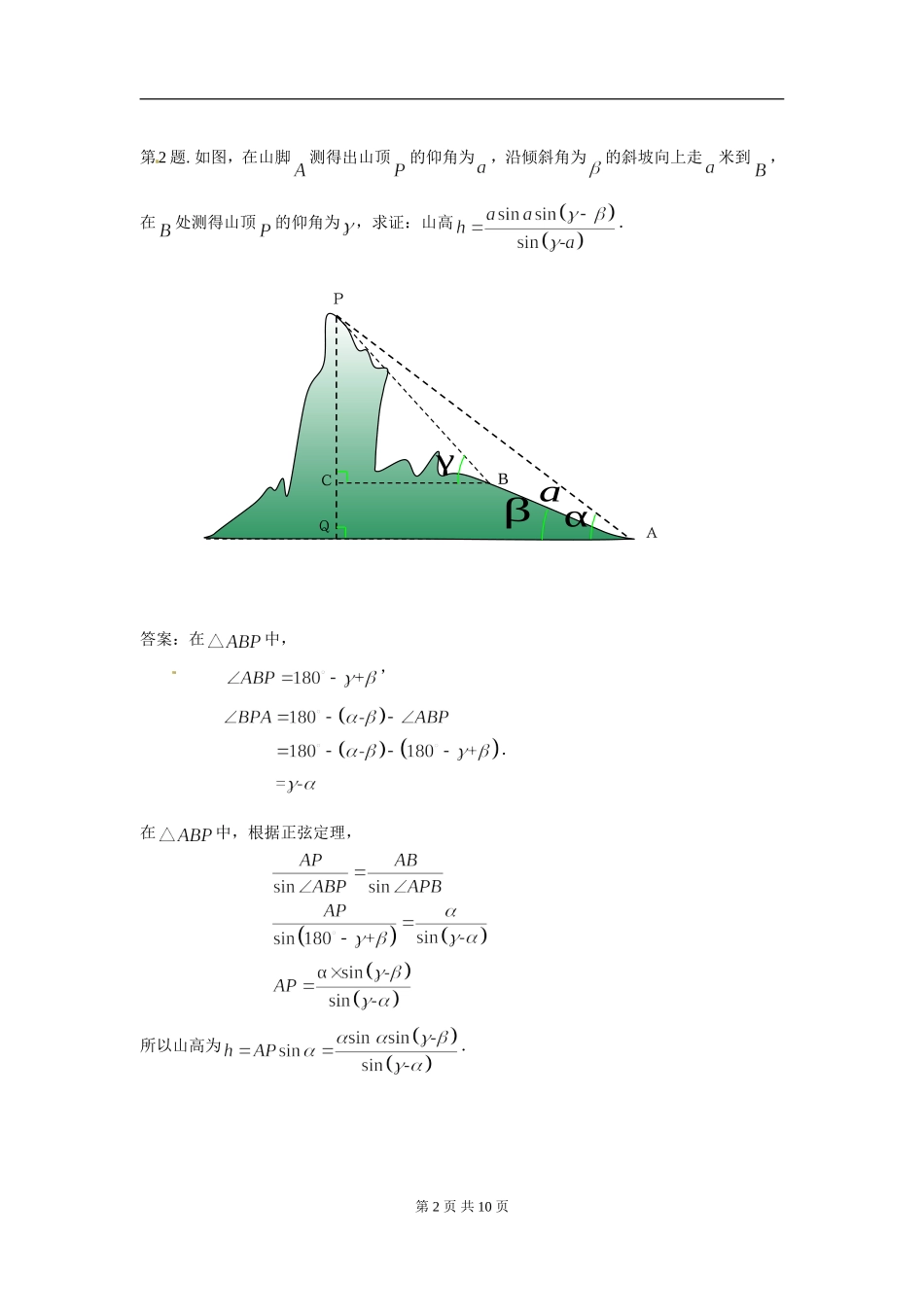
第1题.如图,一艘船以32.2nmile/h的速度向正北航行.在A处看灯塔S在船的北偏东的方向,30min后航行到B处,在B处看灯塔在船的北偏东的方向,已知距离此灯塔6.5nmile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?答案:在中,mile,,根据正弦定理,,,到直线的距离是(cm).所以这艘船可以继续沿正北方向航行.第1页共10页A南北西东65BS第2题.如图,在山脚测得出山顶的仰角为,沿倾斜角为的斜坡向上走米到,在处测得山顶的仰角为,求证:山高.答案:在中,,.在中,根据正弦定理,所以山高为.第2页共10页AQαβaBγCP第3题.测山上石油钻井的井架的高,从山脚测得m,塔顶的仰角是.已知山坡的倾斜角是,求井架的高.答案:在中,m,,,根据正弦定理,井架的高约为9.3m.(6739)第4题.如图,货轮在海上以35nmile/h的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为的方向航行.为了确定船位,在B点观察灯塔A的方位角是,航行半小时后到达C点,观察灯塔A的方位角是.求货轮到达C点时与灯塔A的距离(精确到1nmile).第3页共10页AβαDBCC78126BA答案:在中,=nmile,,,,根据正弦定理,,(nmile).货轮到达C点时与灯塔的距离是约4.29nmile.第5题.轮船A和轮船B在中午12时离开海港C,两艘轮船的航行方向之间的夹角为,轮船A的航行速度是25nmile/h,轮船B的航行速度是15nmile/h,下午2时两船之间的距离是多少?答案:70nmile.第6题.如图,已知一艘船从30nmile/h的速度往北偏东的A岛行驶,计划到达A岛后停留10min后继续驶往B岛,B岛在A岛的北偏西的方向上.船到达C处时是上午10时整,此时测得B岛在北偏西的方向,经过20min到达D处,测得B岛在北偏西的方向,如果一切正常的话,此船何时能到达B岛?答案:在中,第4页共10页304560BCA20min,(nmile),根据正弦定理,,,.在中,,,.根据正弦定理,,就是,(nmile).(nmile).如果这一切正常,此船从C开始到B所需要的时间为:(min)即约1小时26分59秒.所以此船约在11时27分到达B岛.第7题.一架飞机在海拔8000m的高度飞行,在空中测出前下方海岛两侧海岸俯角分别是,计算这个海岛的宽度.第5页共10页8000m2739PQ答案:约5821.71m.第8题.一架飞机从A地飞到B到,两地相距700km.飞行员为了避开某一区域的雷雨云层,从机场起飞后,就沿与原来的飞行方向成角的方向飞行,飞行到中途,再沿与原来的飞行方向成夹角的方向继续飞行直到...