数学：1.3《算法案例---秦九韶算法》测试（新人教A版必修3）.docVIP免费

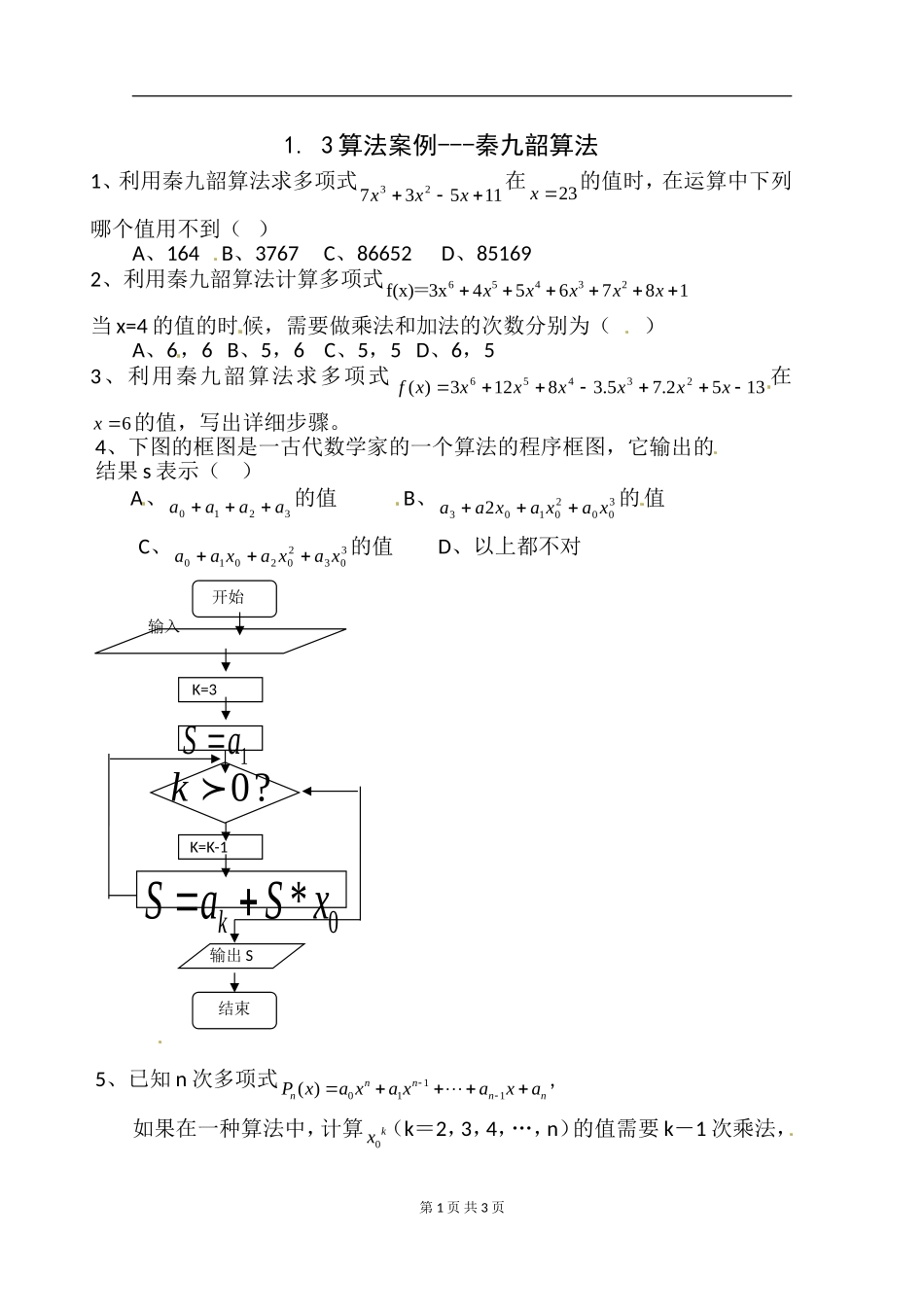
1.3算法案例---秦九韶算法1、利用秦九韶算法求多项式1153723xxx在23x的值时，在运算中下列哪个值用不到（）A、164B、3767C、86652D、851692、利用秦九韶算法计算多项式1876543xf(x)23456xxxxx＝当x=4的值的时候，需要做乘法和加法的次数分别为（）A、6，6B、5，6C、5，5D、6，53、利用秦九韶算法求多项式1352.75.38123)(23456xxxxxxxf在6x的值，写出详细步骤。4、下图的框图是一古代数学家的一个算法的程序框图，它输出的结果s表示（）A、3210aaaa的值B、300201032xaxaxaa的值C、303202010xaxaxaa的值D、以上都不对5、已知n次多项式1011()nnnnnPxaxaxaxa,如果在一种算法中，计算0kx（k＝2，3，4，…，n）的值需要k－1次乘法，第1页共3页开始K=31aS?0kK=K-10*xSaSk输入输出S结束（1）计算30()Px的值需要9次运算（6次乘法，3次加法），那么计算0()nPx的值需要多少次运算？（2）若采取秦九韶算法：0011(),()()kkkPxaPxxPxa（k＝0，1，2，…，n－1），计算30()Px的值只需6次运算，那么计算0()nPx的值共需要多少次运算？（3）若采取秦九韶算法，设ai=i+1，i=0，1，…，n，求P5（2）（写出采取秦九韶算法的计算过程）答案：1、D2、A3、解：13)5)2.7)5.3)8)123((((()(xxxxxxxf第2页共3页2.243168)6(2.2431681362.40530562.67542.765.11245.36188863012635645342312010fvvvvvvvvvvvvv4、C5、n＋3)（2）2n；（3）∵0011(),()()kkkPxaPxxPxa，∴P0（2）=1，P1（2）=2P0（2）+2=4；P2（2）=2P1（2）+3=11；P3（2）=2P2（2）+4=26；P4（2）=2P3（2）+5=57；P5（2）=2P4（2）+6=120第3页共3页