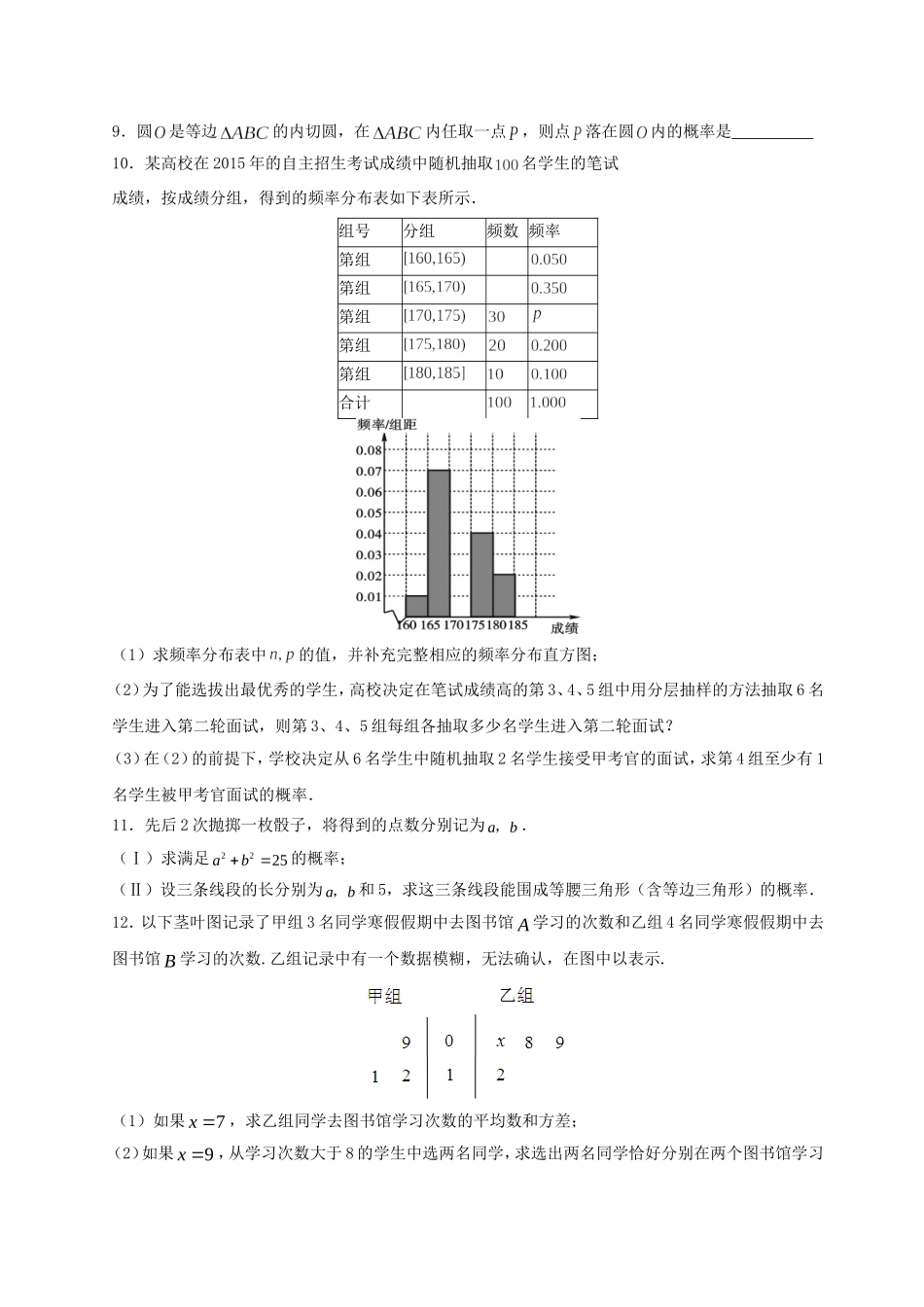
第三章概率1.随机事件的概率及概率的意义必然事件、不可能事件、确定事件、随机事件、频数与频率2、概率的基本性质:1)必然事件概率为1,不可能事件概率为0,因此0≤P(A)≤1;2)当事件A与B互斥时,满足加法公式:P(A∪B)=P(A)+P(B);3)若事件A与B为对立事件,则A∪B为必然事件,所以P(A∪B)=P(A)+P(B)=1,于是有P(A)=1—P(B);4),3.古典概型及随机数的产生(1)古典概型的使用条件:试验结果的有限性和所有结果的等可能性。(2)古典概型的解题步骤;①求出总的基本事件数与A事件所包含的基本事件数;②利用公式求解.4.几何概型(1)几何概型的特点:(1)试验中所有可能出现的结果(基本事件)有无限多个;(2)每个基本事件出现的可能性相等(2)几何概型的概率公式:;想一想互斥事件与对立事件的区别与联系是什么?练一练1.抛掷红、蓝两颗骰子,若已知蓝骰子点数为3或6时,则两颗骰子点数之和大于8的概率为()A.B.C.D.2.现有名女教师和名男教师参加说题比赛,共有道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为()A.13B.23C.12D.343.甲乙两人有三个不同的学习小组A,B,C可以参加,若每人必须参加并且仅能参加一个学习小组,则两人参加同一个小组的概率为()A.13B.14C.15D.164.在区间1m,上随机选取一个数,若1x的概率为25,则实数m的值为()A.2B.3C.4D.55.《九章算术》中有如下问题:“今有勾八步,股一十五步,问勾中容圆,径几何?”其大意:“已知直角三角形两直角边长分别为步和15步,问其内切圆的直径为多少步?”现若向此三角形内随机投一粒豆子,则豆子落在其内切圆外的概率是()A.310B.320C.3110D.31206.某学校上午安排上四节课,每节课时间为40分钟,第一节课上课时间为8:00~8:40,课间休息10分钟.某学生因故迟到,若他在9:10~10:00之间到达教室,则他听第二节课的时间不少于10分钟的概率为()A.15B.310C.25D.457.如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在CEF内的概率为()A.B.C.D.8.在区间3,2上随机取一个数,则事件“1142x”发生的概率为________.9.圆是等边的内切圆,在内任取一点,则点落在圆内的概率是10.某高校在2015年的自主招生考试成绩中随机抽取名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.组号分...