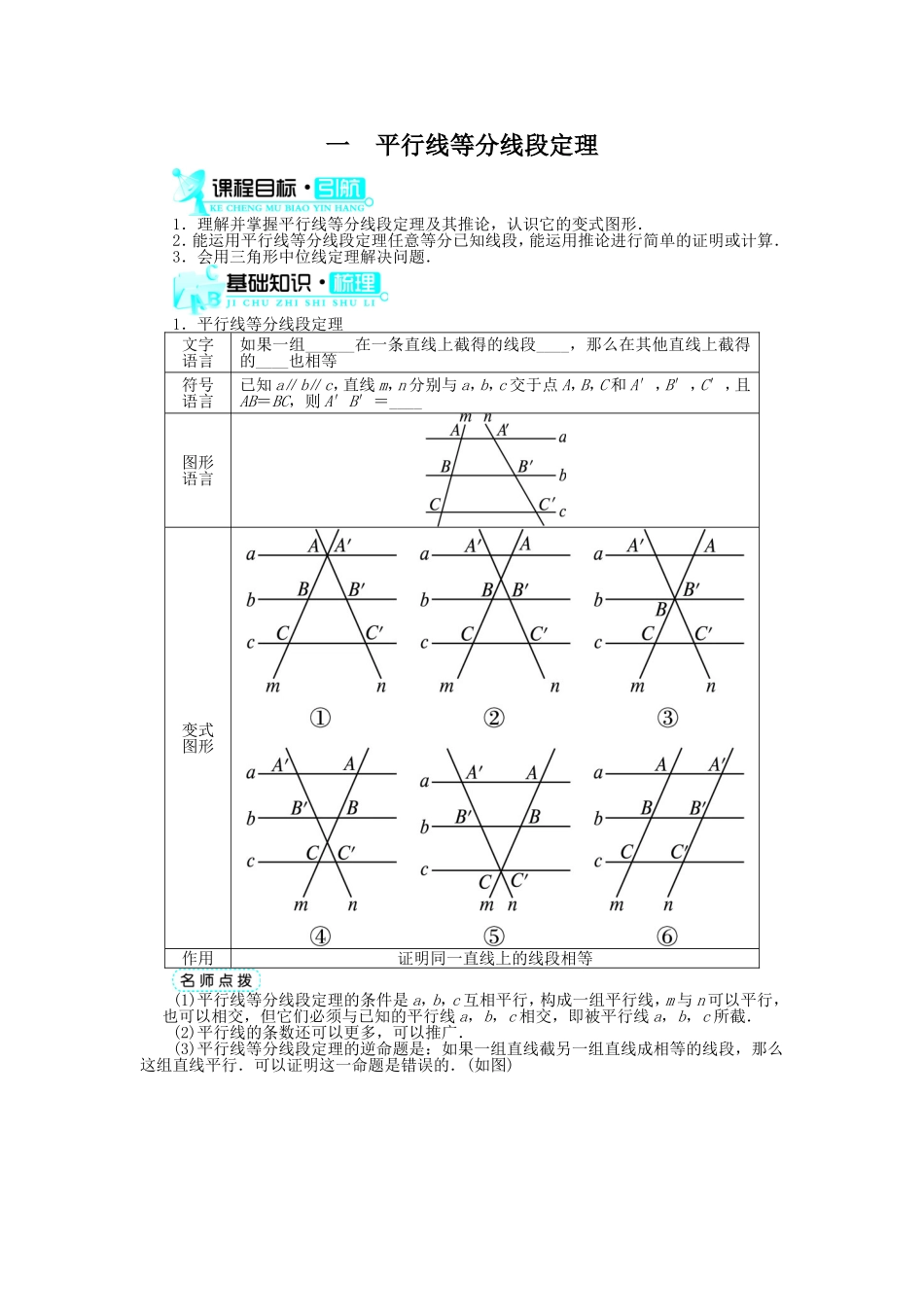
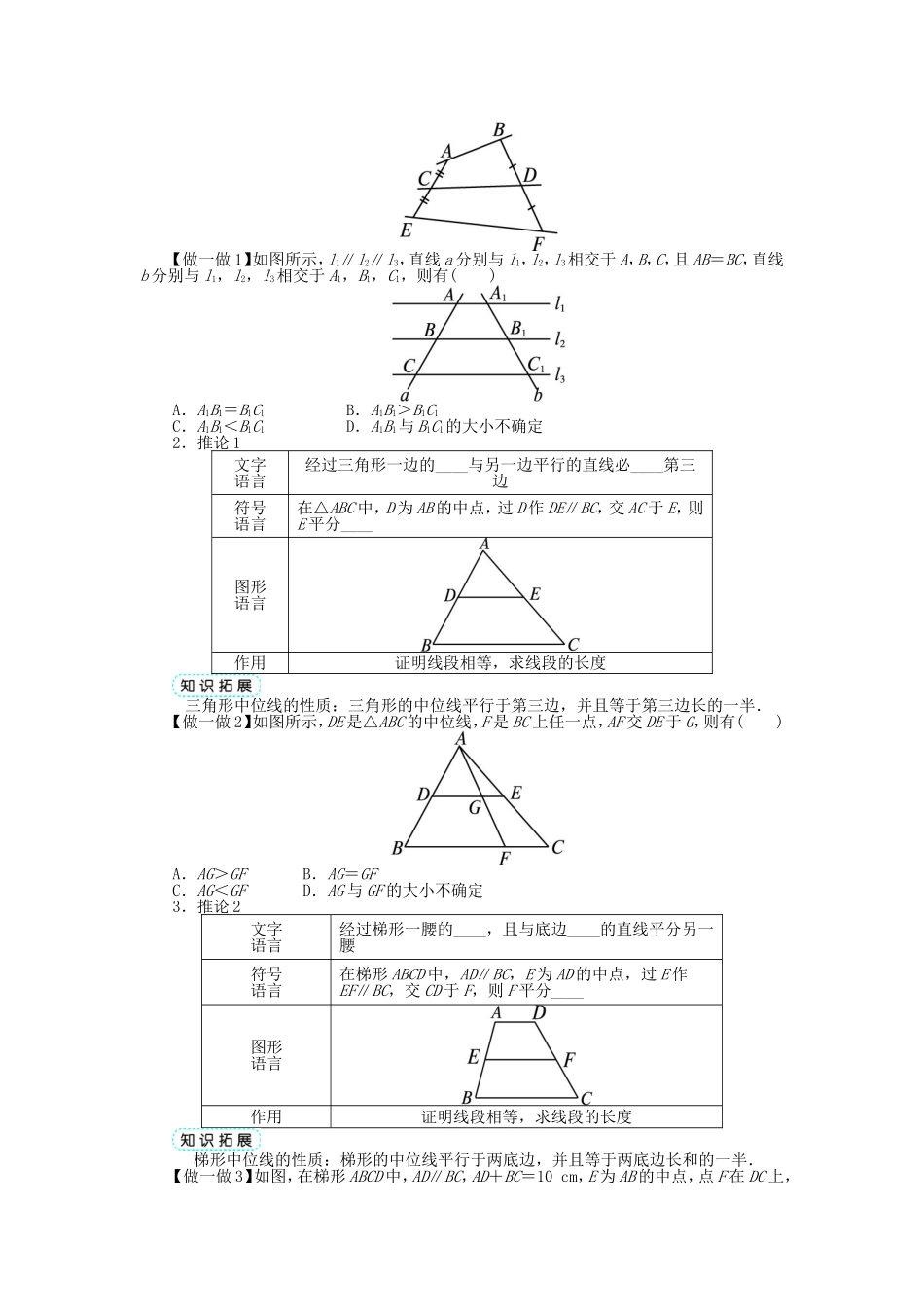
一平行线等分线段定理1.理解并掌握平行线等分线段定理及其推论,认识它的变式图形.2.能运用平行线等分线段定理任意等分已知线段,能运用推论进行简单的证明或计算.3.会用三角形中位线定理解决问题.1.平行线等分线段定理文字语言如果一组______在一条直线上截得的线段____,那么在其他直线上截得的____也相等符号语言已知a∥b∥c,直线m,n分别与a,b,c交于点A,B,C和A′,B′,C′,且AB=BC,则A′B′=____图形语言变式图形作用证明同一直线上的线段相等(1)平行线等分线段定理的条件是a,b,c互相平行,构成一组平行线,m与n可以平行,也可以相交,但它们必须与已知的平行线a,b,c相交,即被平行线a,b,c所截.(2)平行线的条数还可以更多,可以推广.(3)平行线等分线段定理的逆命题是:如果一组直线截另一组直线成相等的线段,那么这组直线平行.可以证明这一命题是错误的.(如图)【做一做1】如图所示,l1∥l2∥l3,直线a分别与l1,l2,l3相交于A,B,C,且AB=BC,直线b分别与l1,l2,l3相交于A1,B1,C1,则有()A.A1B1=B1C1B.A1B1>B1C1C.A1B1<B1C1D.A1B1与B1C1的大小不确定2.推论1文字语言经过三角形一边的____与另一边平行的直线必____第三边符号语言在△ABC中,D为AB的中点,过D作DE∥BC,交AC于E,则E平分____图形语言作用证明线段相等,求线段的长度三角形中位线的性质:三角形的中位线平行于第三边,并且等于第三边长的一半.【做一做2】如图所示,DE是△ABC的中位线,F是BC上任一点,AF交DE于G,则有()A.AG>GFB.AG=GFC.AG<GFD.AG与GF的大小不确定3.推论2文字语言经过梯形一腰的____,且与底边____的直线平分另一腰符号语言在梯形ABCD中,AD∥BC,E为AD的中点,过E作EF∥BC,交CD于F,则F平分____图形语言作用证明线段相等,求线段的长度梯形中位线的性质:梯形的中位线平行于两底边,并且等于两底边长和的一半.【做一做3】如图,在梯形ABCD中,AD∥BC,AD+BC=10cm,E为AB的中点,点F在DC上,且EF∥AD,则EF的长为()A.5cmB.10cmC.20cmD.不确定答案:1.平行线相等线段B′C′【做一做1】A l1∥l2∥l3,AB=BC,∴A1B1=B1C1.2.中点平分AC【做一做2】B DE是△ABC的中位线,∴在△ABF中,DG∥BF,又 AD=DB,∴G平分AF,即AG=GF.3.中点平行CD【做一做3】A由推论2知,EF是梯形ABCD的中位线,则EF=(AD+BC)=×10=5(cm).平行线等分线段定理的两个推论的证明剖析:(1)推论1:如图①,在△ABC中,B′...