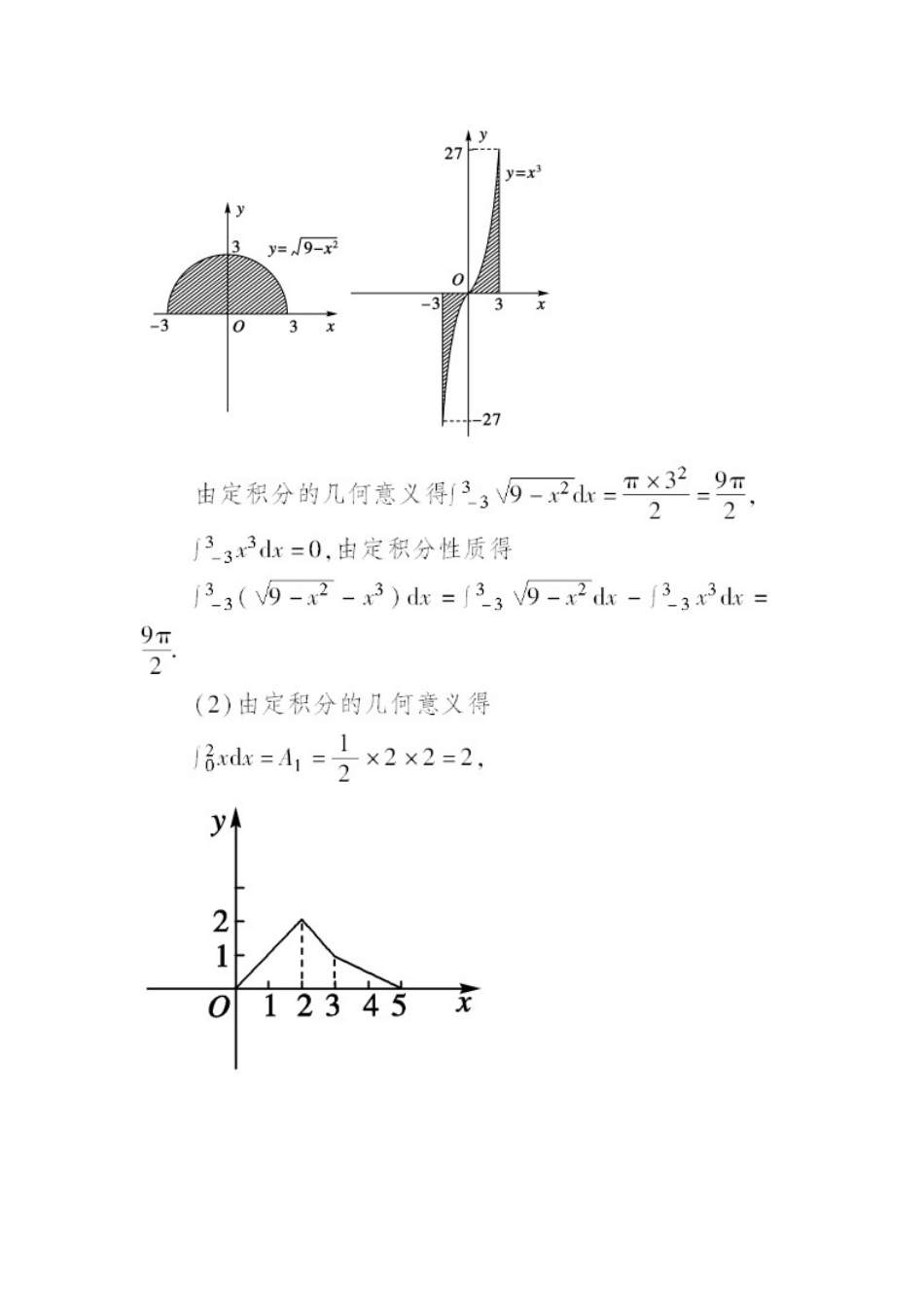
1.5.3定积分的概念考点一:根据定积分的定义求定积分1、求x3dx.[解析](1)分割[0,1]:0<<<…<<=1.(2)近似代替:作和3·+3·+…+3·.=3·.(因为x3连续,所以ξi可随意取而不影响极限,故我们此处将ξi取为[xi,xi+1]的右端点也无妨)(3)取极限:3·=3=2=,∴x3dx=limn→∞=.(此处用到了求和公式13+23+…+n3=(1+2+…+n)2=2)因此x3dx=.2、利用定积分的定义求2dx的值.[解析]令f(x)=2.(1)分割:在区间[a,b]上等间隔插入(n-1)个分点,把区间[a,b]等分成n个小区间(i=1,2,…,n),每个小区间的长度为.(2)近似代替、作和:取ξi=a+(i=1,2,…,n),则Sn=·==2(b-a).(3)取极限:2dx=limn→∞Sn=limn→∞2(b-a)=2(b-a).考点二:根据定积分的几何意义求定积分1、求-1(x3+3x)dx.[解析]∵y=x3+3x为[-1,1]上的奇函数,图象关于原点对称,∴曲边梯形在x轴上方部分面积与在x轴下方部分面积相等,由积分的几何意义知(x3+3x)dx=0.2、用定积分的意义求值[解析](1)由直线x=-1,x=3,y=0以及y=3x+1所围成的图形,如图所示:表示由直线x=-1,x=3,y=0以及y=3x+1所围成的图形在x轴上方的面积减去在x轴下方的面积,∴=××(3×3+1)-·2=-=16.考点三:利用性质求定积分1、(1)计算的值(2)已知,求在区间上的定积分[解析](1)如图,考点四:利用定积分表示平面图形的面积1、利用定积分的性质和定义表示下列曲线围成的平面区域的面积.(1)y=0,y=,x=2;(2)y=x-2,x=y2.[解析](1)曲线所围成的区域如图(1)所示,设此面积为S,则S=(-0)dx=dx(2)曲线所围成的平面区域如图(2)所示,S=A1+A2,A1由y=,y=-,x=1围成;A2由y=,y=x-2,x=1和x=4围成.∴A1=[-(-)]dx,A2=[-(x-2)]dx,∴S=2dx+(-x+2)dx.2、画出下列曲线围成的平面区域并用定积分表示其面积.(1)y=|sinx|,y=0,x=2,x=5.(2)y=logx,y=0,x=,x=3.[解析](1)曲线所围成的平面区域如图所示.设此面积为S,则S=|sinx|dx或S=sinxdx+(-sinx)dx=sinxdx-πsinxdx.