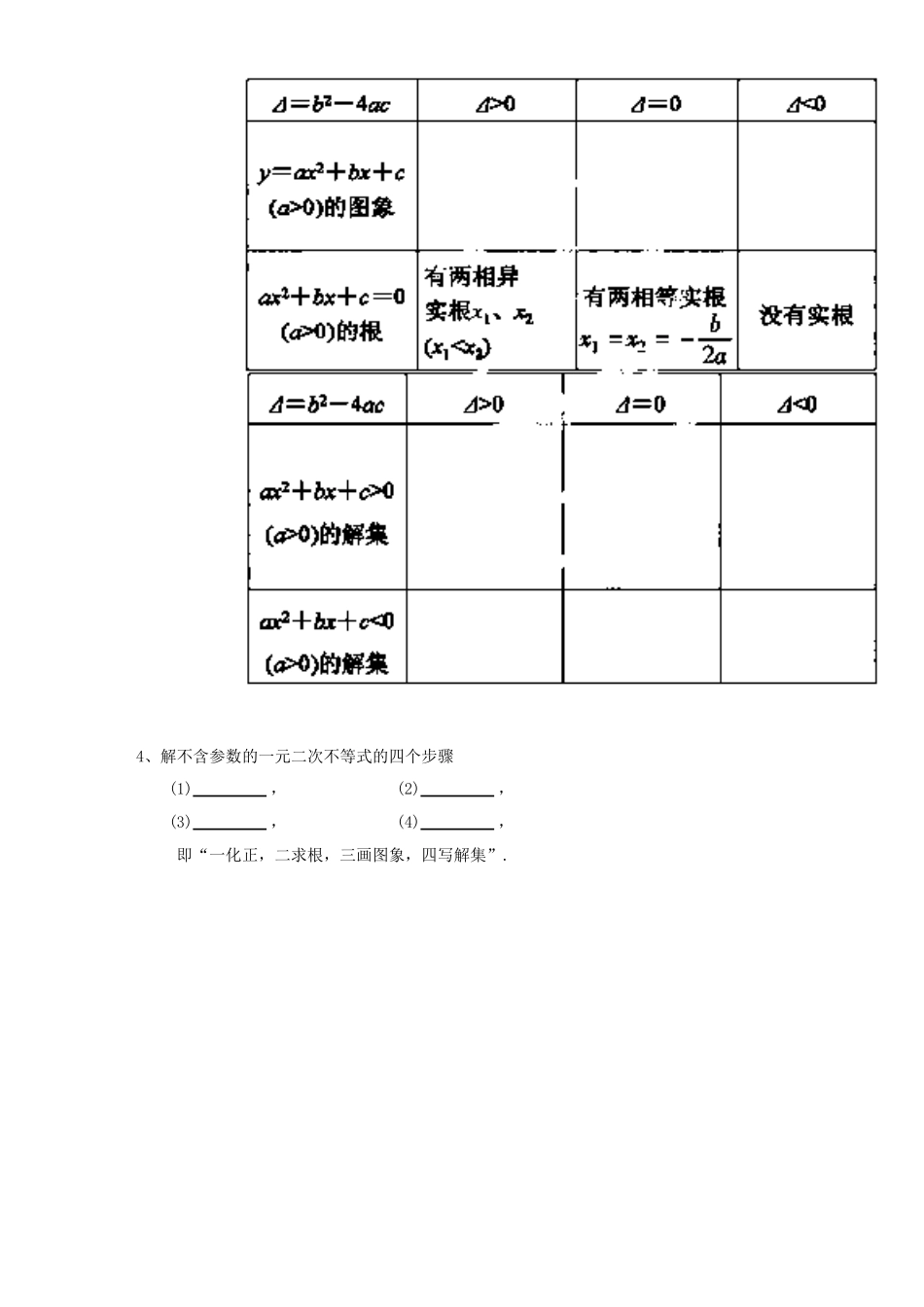
☆学习目标☆1.能够进行较简单地分类讨论,求解简单的含字母参数的一元二次不等式.2.能够根据三个二次之间的关系,解决与一元二次不等式有关的恒成立问题。☆学习重点☆1.能够进行较简单地分类讨论,求解简单的含字母参数的一元二次不等式.2.能够根据三个二次之间的关系,解决与一元二次不等式有关的恒成立问题。☆学习难点☆1.能够根据三个二次之间的关系,解决与一元二次不等式有关的恒成立问题。☆基础回扣☆1、只含有_____未知数,并且未知数的最高次数是__的不等式,称为一元二次不等式.2、一元二次不等式的一般表达式为:,3、一元二次不等式、一元二次方程、二次函数三者之间的关系4、解不含参数的一元二次不等式的四个步骤(1),(2),(3),(4),即“一化正,二求根,三画图象,四写解集”.☆问题探讨与解题研究☆类型一含参数的一元二次不等式的解法例1.解关于x的不等式:ax2-2x+1>0.解析:①当a=0时,不等式即-2x+1>0,∴解集为{x|x<};②当a<0时,△=4-4a>0,此时不等式为x2-x+<0,由于方程x2-x+=0的两根分别为、,且>,∴不等式的解集为:{x|<x<};③当a>0时,若0<a<1,此时不等式即x2-x+>0, <,∴不等式解集为{x|x<,或x>},若a=1,则不等式为(x-1)2>0,∴不等式解集为{x∈R|x≠1};若a>1,则△<0,不等式解集为R.例2.解关于x的不等式-(a+)x+<0(a∈R).【小结】解含参数的一元二次不等式的三个步骤(1)当不等式的二次项系数不确定时,要分二次项系数等于0,大于0,小于0三种情况进行分类.(2)当二次项系数的正负确定后,再按判别式等于0,大于0,小于0三种情况分类.(3)当判别式确定后,要根据两根的大小分类讨论.类型二不等式恒成立问题1.如果关于x的不等式对一切实数x都成立,则k的取值范围是_________.2.当a为何值时,不等式的解集是全体实数?【练习】若关于x的不等式a+2x+2>0在R上恒成立,求实数a的取值范围.☆课堂检测☆1.若“00的解集是__________.解析:由>0,得(x+3)(x-3)(x-2)>0(x≠2),由数轴标根法,易得-33.3.(2012·福建卷)已知关于x的不等式x2-ax+2a>0在R上恒成立,则实数a的取值...