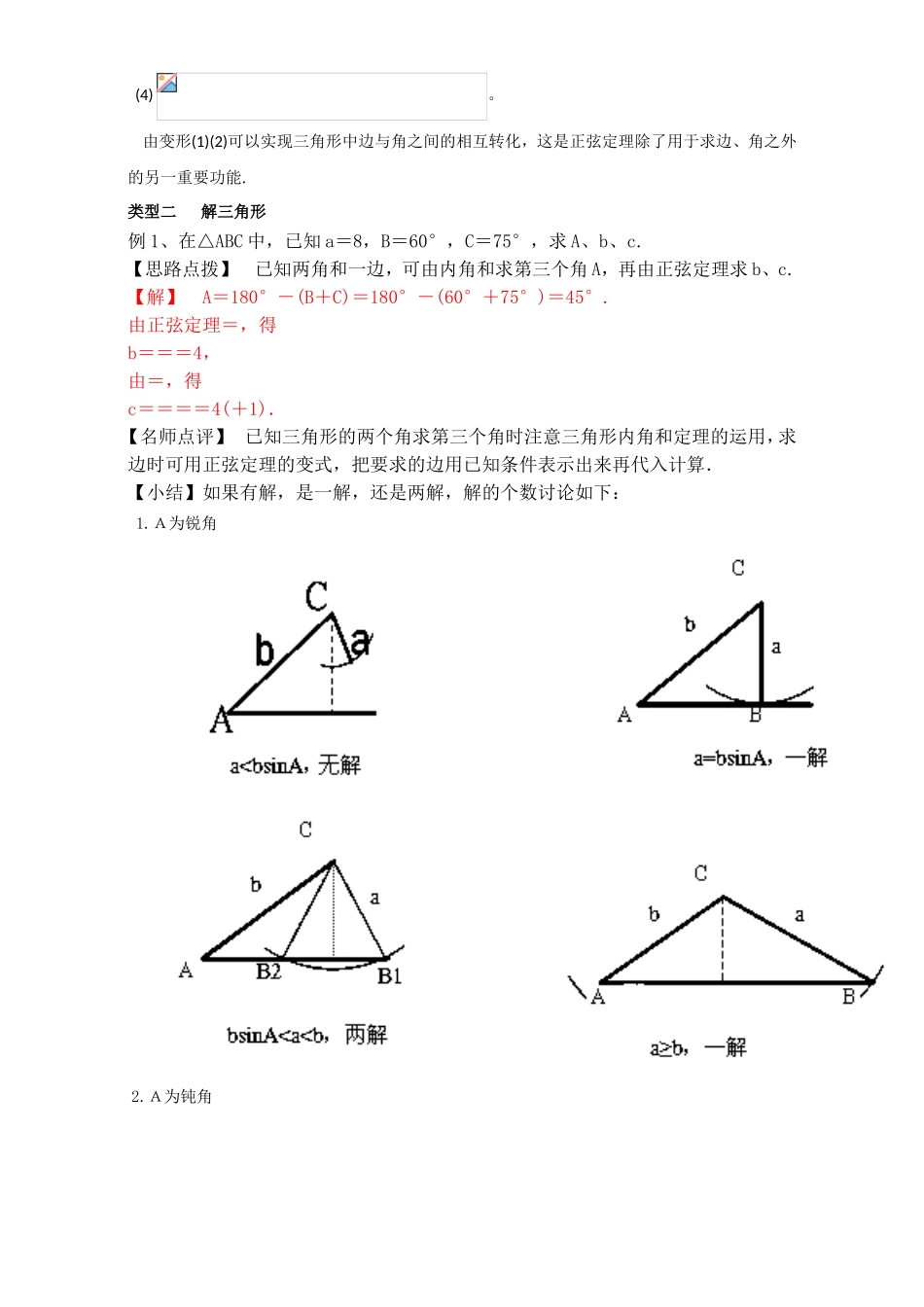
☆教学目标☆1.了解正弦定理的推导过程.2.理解并掌握正弦定理的内容,能运用正弦定理解决两类解三角形的问题.3.通过正弦定理的学习,体会“数形结合”和“转化与化归”的数学思想.☆学习重点☆1.正弦定理的证明及它在化简和求值中的应用。☆学习难点☆1.正弦定理的探索和证明;2.正弦定理在化简和求值中的应用以及已知两边及其中一边的对角解三角形时解的个数的判断。☆基础回扣☆1.正弦定理:在△ABC中,角A,B,C所对的边分别为a,b,c.(1)各边和它所对角的正弦的比相等,===2R(R为外接圆半径).变形形式有:a=;b=;c=;sinA∶sinB∶sinCgkstk=∶∶.,,2RsinB,2RsinA,2RsinC,b;c;a.2.正弦定理在解三角形中的应用①已知两边及其中一边的,求其他的边和角;②已知两角及,求其他的边和角.对角,一边☆问题探讨与解题研究☆类型一与正弦定理有关的推论例1、想一想:如何用△ABC的外接圆证明这一定理?分析:作△ABC的外接圆,在△ABC中,令BC=a,AC=b,AB=c,根据直径所对的圆周角是直角以及同弧所对的圆周角相等,来证明这一关系.【练习】1.在△ABC中,角A,B,C的对边分别是a,b,c,若A∶B∶C=1∶2∶3,则a∶b∶c等于()(A)1∶2∶3(B)2∶3∶4(C)3∶4∶5(D)1∶∶22.在△ABC中,A=60°,a=3,则()(A)(B)(C)(D)【小结】正弦定理的常用变形(1)a=2RsinA,b=2RsinB,c=2RsinC;(2);(3)a∶b∶c=sinA∶sinB∶sinC;(4)。由变形(1)(2)可以实现三角形中边与角之间的相互转化,这是正弦定理除了用于求边、角之外的另一重要功能.类型二解三角形例1、在△ABC中,已知a=8,B=60°,C=75°,求A、b、c.【思路点拨】已知两角和一边,可由内角和求第三个角A,再由正弦定理求b、c.【解】A=180°-(B+C)=180°-(60°+75°)=45°.由正弦定理=,得b===4,由=,得c====4(+1).【名师点评】已知三角形的两个角求第三个角时注意三角形内角和定理的运用,求边时可用正弦定理的变式,把要求的边用已知条件表示出来再代入计算.【小结】如果有解,是一解,还是两解,解的个数讨论如下:1.A为锐角2.A为钝角3.A为直角时,与A为钝角相同,a>b时,一解;a≤b时,无解.【练习】1、在△ABC中,,则B=()(A)(B)(C)或(D)或2、已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=,A+C=2B,则sinC等于()(A)(B)(C)(D)类型三判定三角形的形状问题【例1】在△ABC中,若sinA=2sinBcosC,且sin2A=sin2B+sin2C,试判断△ABC的形状.【思路点拨】利用正弦定理将...