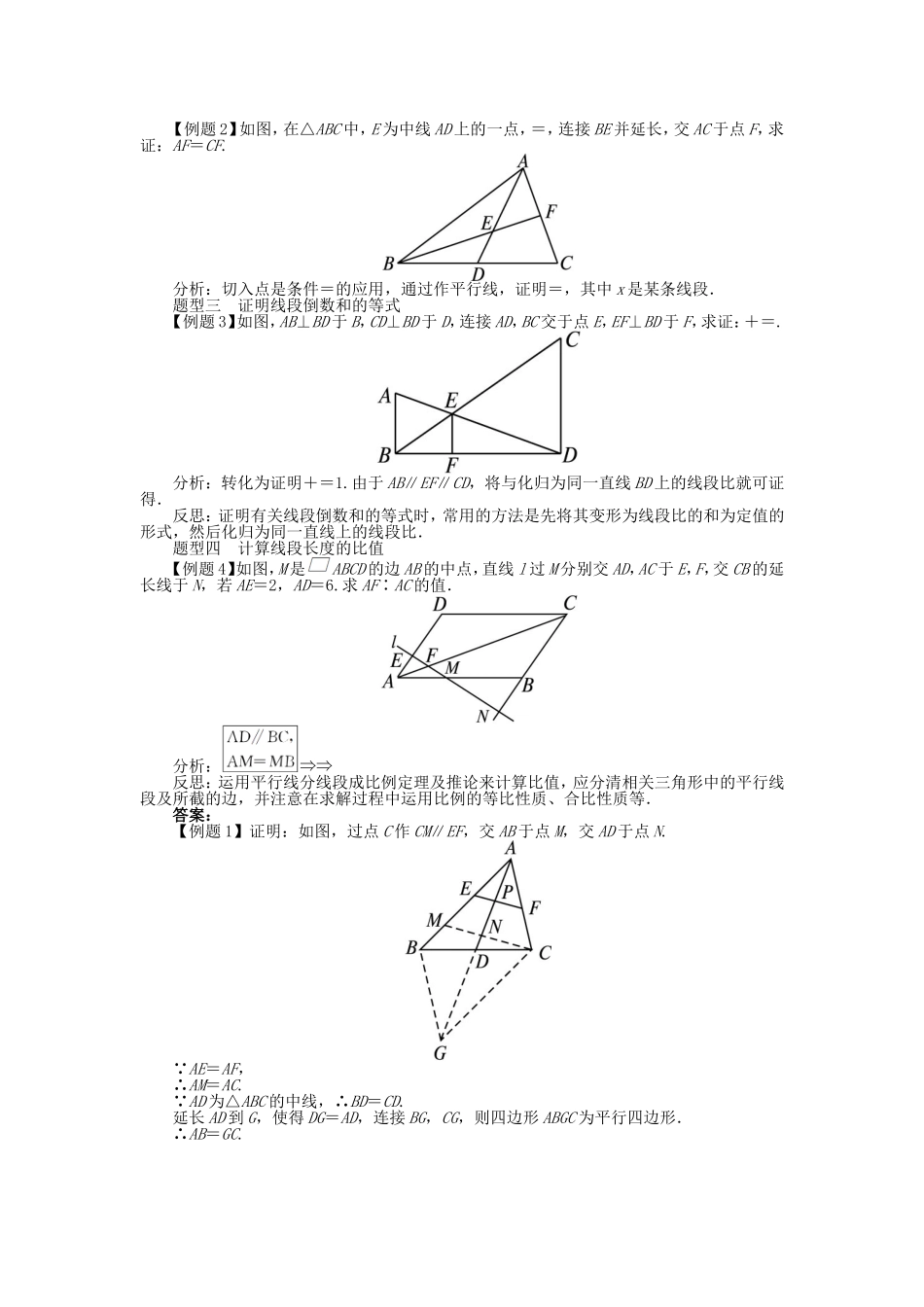
二平行线分线段成比例定理1.掌握平行线分线段成比例定理及其推论.2.能利用平行线分线段成比例定理及推论解决有关问题.1.平行线分线段成比例定理文字语言三条平行线截两条直线,所得的对应线段______符号语言a∥b∥c,直线m分别与a,b,c相交于点A,B,C,直线n分别与a,b,c相交于点D,E,F,则=____图形语言作用证明分别在两条直线上的线段成比例(1)定理的条件与平行线等分线段定理的条件相同,它需要a,b,c互相平行,构成一组平行线,m与n可以平行,也可以相交,但它们必须与已知的平行线a,b,c相交,即被平行线a,b,c所截.平行线的条数还可以更多.(2)定理的结论还有=,=等.可以归纳为=,=等,便于记忆.(3)当截得的对应线段成比例,且比值为1时,则截得的线段相等,因此平行线分线段成比例定理是平行线等分线段定理的扩充,而平行线等分线段定理是平行线分线段成比例定理的特例;平行线等分线段定理是证明线段相等的依据,而平行线分线段成比例定理是证明线段成比例的途径.【做一做1】如图所示,a∥b∥c,AB=2,BC=3,则等于()A.B.C.D.2.推论文字语言平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段______符号语言直线DE分别与△ABC的两边AB,AC所在直线交于D,E,且DE∥BC,则=____图形语言作用证明三角形中的线段成比例【做一做2-1】如图所示,在△ABC中,DE∥BC,若AD=3,BD=1,则等于()A.1B.3C.D.【做一做2-2】如图,AB∥CD,AC,BD相交于O点,BO=7,DO=3,AC=25,则AO的长为()A.10B.12.5C.15D.17.5答案:1.成比例【做一做1】B a∥b∥c,∴==.2.成比例【做一做2-1】D DE∥BC,∴====.【做一做2-2】D AB∥CD,∴==,∴=,∴AO=AC=×25==17.5.比例的概念及有关性质剖析:(1)线段的比:用同一个长度单位去量两条线段,所得的长度比叫做这两条线段的比.(2)比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段.(3)比例的有关概念:已知四条线段a,b,c,d,如果=或a∶b=c∶d,那么线段a,d叫做比例外项,线段b,c叫做比例内项,线段d叫做线段a,b,c的第四比例项.若=或b2=ac,那么线段b叫做线段a,c的比例中项.(4)比例的性质:①基本性质:a∶b=c∶d⇔ad=bc.②合比性质:如果=,那么=.③等比性质:如果==…=(b+d+…+n≠0),那么=.(5)线段的比与比例线段是既有区别又有联系的两个...