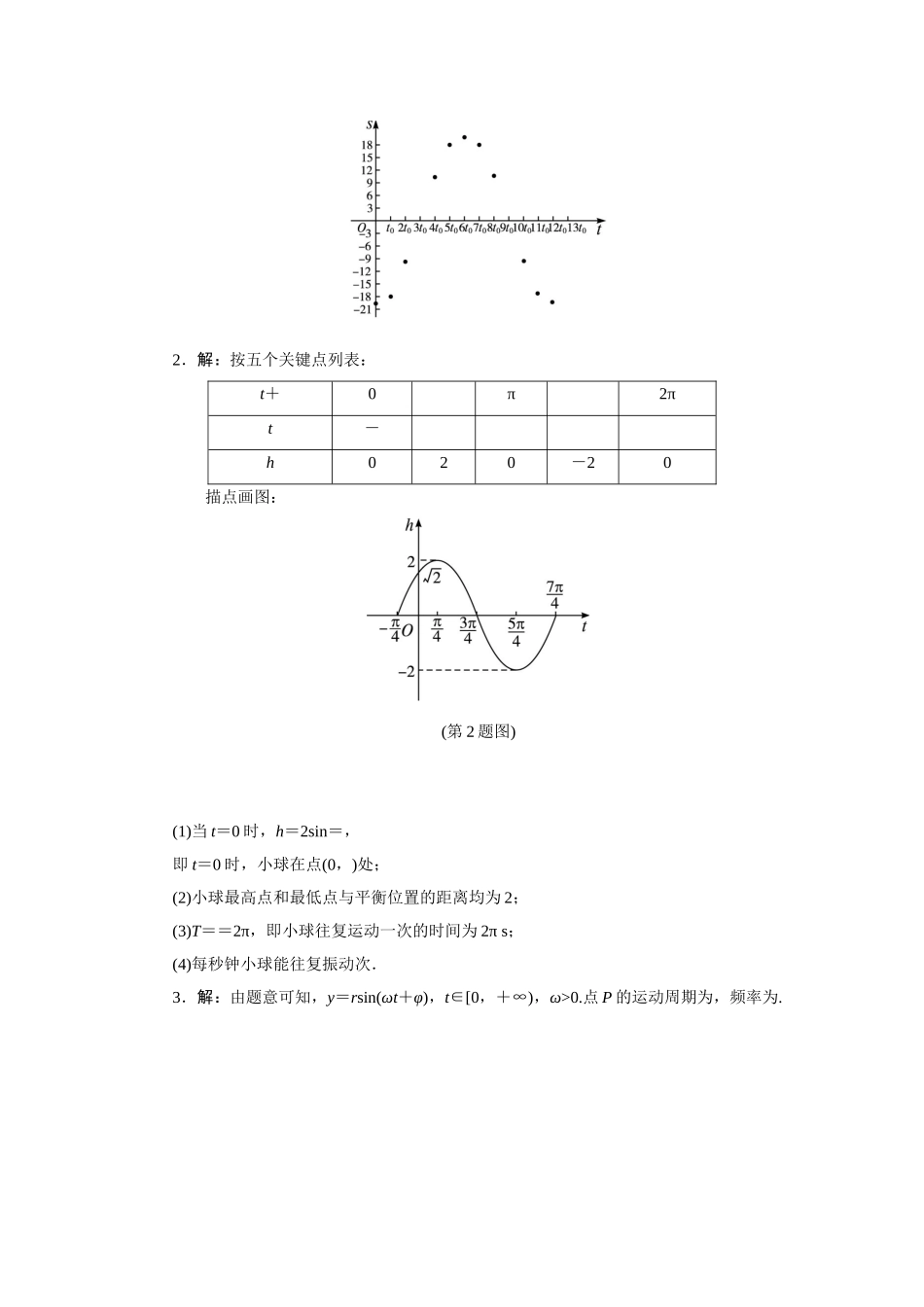
教材习题点拨练习1.解:(第1题图)2.(1)C(2)B(3)C3.解:振幅是,周期是4π,频率是.先把y=sinx图象上所有的点向右平行移动个单位长度,得到y=sin的图象;再把y=sin图象上所有点的横坐标伸长到原来的2倍,得到y=sin的图象;再把y=sin图象上所有点的纵坐标缩短到原来的倍,得到y=sin的图象.4.解:初相是.把y=sinx图象上所有的点向左平行移动个单位长度,便可得到y=sin的图象,注意x∈[0,+∞),并非实数集.习题1.5A组1.(1)C(2)A(3)D2.解:(第2题图)3.解:(1)振幅是8,周期是8π,初相是-.先把正弦曲线向右平移个单位长度,得到y1=sin,x∈R的图象;再把函数y1的图象上所有点的横坐标伸长到原来的4倍(纵坐标不变),得到函数y2=sin,x∈R的图象;再把函数y2的图象上所有点的纵坐标伸长到原来的8倍(横坐标不变),得到y3=8sin,x∈R的图象;最后把y3的图象在y轴左侧的部分抹去,就得到函数y=8sin,x∈[0,+∞)的图象.(2)振幅是,周期是,初相是.先把正弦曲线向左平移个单位长度,得到函数y1=sin,x∈R的图象;再把函数y1的图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得到y2=sin,x∈R的图象;再把y2的图象上所有点的纵坐标缩短到原来的倍(横坐标不变),得到函数y3=sin,x∈R的图象;最后把y3的图象在y轴左侧的部分抹去,就得到函数y=sin,x∈[0,+∞)的图象.4.解:(1)周期为0.02s,频率为50,振幅为5,初相为.(2)当t=0时,i=;当t=时,i=5;当t=时,i=0;当t=时,i=-5;当t=时,i=0.5.解:(1)2π;(2)约24.8cm.B组1.解:根据已知数据作出散点图(如答图),由散点图可知,振子的振动函数解析式为s=20sin,t∈[0,+∞).2.解:按五个关键点列表:t+0π2πt-h020-20描点画图:(第2题图)(1)当t=0时,h=2sin=,即t=0时,小球在点(0,)处;(2)小球最高点和最低点与平衡位置的距离均为2;(3)T==2π,即小球往复运动一次的时间为2πs;(4)每秒钟小球能往复振动次.3.解:由题意可知,y=rsin(ωt+φ),t∈[0,+∞),ω>0.点P的运动周期为,频率为.