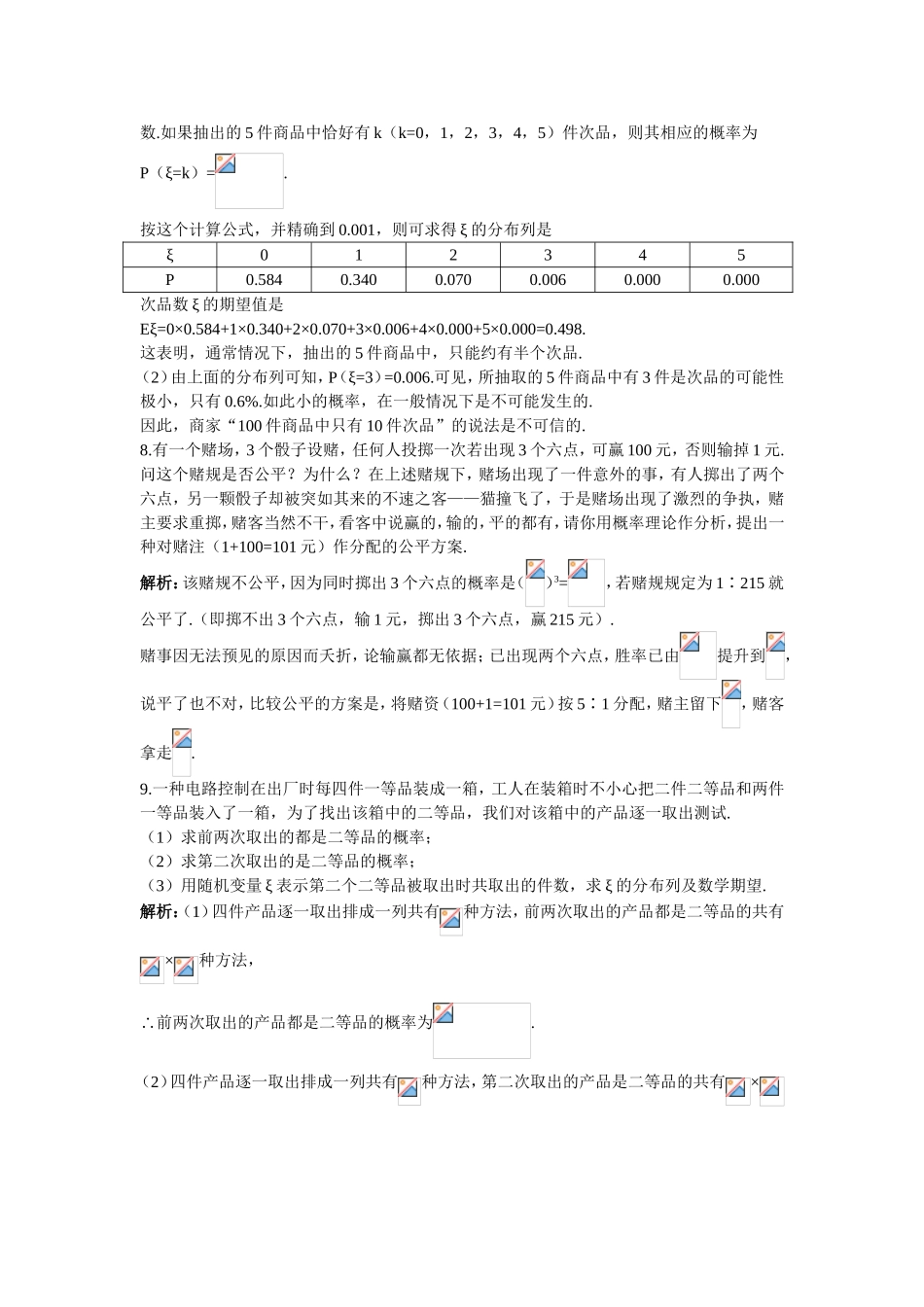
课后导练基础达标1.袋中有7个白球,3个红球,现采取不放回方式取球,直到取到红球为止.以ξ表示取球次数,则Eξ=()A.B.C.D.答案:A2.某随机变量ξ的概率分布为:ξ0123P0.1ab0.1且Eξ=1.5,则a=_________,b=_________.答案:a=b=0.43.已知盒中有10个灯泡,其中8个正品,2个次品.需要从中取出2个正品,每次取出1个,取出后不放回,直到取出2个正品为止,设ξ为取出的次数,求ξ的分布列及Eξ.解析:每次取1件产品,∴至少需2次,即ξ最小为2,有2件次品,当前2次取得的都是次品时,ξ=4,所以ξ可以取2,3,4.P(ξ=2)=;P(ξ=3)=;P(ξ=4)=1-.ξ∴的分布列如下:Ξ234PEξ=2×P(ξ=2)+3×P(ξ=3)+4×P(ξ=4)=.4.某工厂对2月份的奖金发放作出了如下规定:在这四周时间里有1周完成生产任务,则得奖金48元;如果有2周完成生产任务,则可得奖金80元;如果有3周完成生产任务,则可得奖金128元;如果4周都完成了生产任务,则可得奖金160元;如果4周都未完成任务,则没有奖金,假设某工人每周完成任务与否是等可能的,求一工人在2月份所得奖金的期望.解析:设该工人在2月份所得奖金为ξ,他每周完成任务的概率为,P(ξ=0)=()0()4=,P(ξ=48)=()1()3=P(ξ=80)=()2()2=P(ξ=128)=()3()=P(ξ=160)=()4=Eξ=0×∴+48×+80×+128×+160×=84.5.甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6道,乙能答对其中的8道,规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.(1)求甲答对的试题数ξ的概率分布及数学期望.(2)求甲、乙两人至少有一人考试合格的概率.解析:(1)ξ的分布列如下:ξ0123P甲答对试题数ξ的数学期望Eξ=0×+1×+2×+3×=.(2)设甲、乙两人考试合格的事件分别为A,B,则P(A)=,P(B)=,∴甲、乙两人考试均不合格的概率为:P(·)=P()P()=(1-)·(1-)=∴甲、乙两人至少有一人考试合格的概率为P=1-P(·)=1-=综合运用6.某保险公司新开设了一项保险业务,若在一年内事件E发生,该公司要赔偿a元,设在一年内E发生的概率为P,为使公司收益的期望值等于a的百分之十,公司应要求顾客交多少保险金?解析:设保险公司要求赔偿顾客交x元保险金,若以ξ表示公司每年的收益额,则ξ的分布列为:ξxx-aP1-pp 公司每年收益ξ的期望值为Eξ=x(1-p)+(x-a)p=x-ap要使公司收益的期望值等于a的百分之十,只需Eξ=0.1a,即x-ap=0.1a,x=(0.1+p)a,∴...