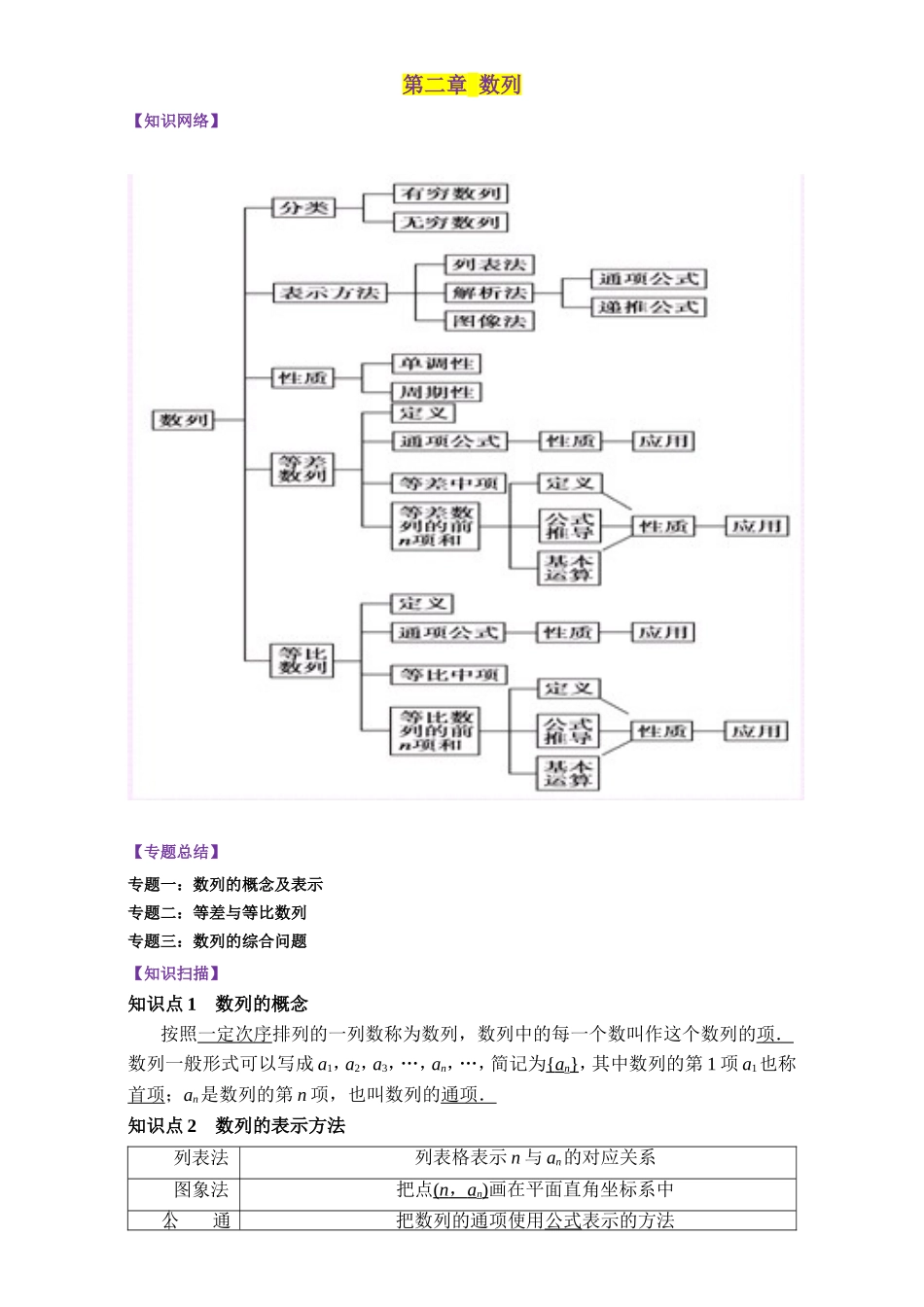
第二章数列【知识网络】【专题总结】专题一:数列的概念及表示专题二:等差与等比数列专题三:数列的综合问题【知识扫描】知识点1数列的概念按照一定次序排列的一列数称为数列,数列中的每一个数叫作这个数列的项.数列一般形式可以写成a1,a2,a3,…,an,…,简记为{an},其中数列的第1项a1也称首项;an是数列的第n项,也叫数列的通项.知识点2数列的表示方法列表法列表格表示n与an的对应关系图象法把点(n,an)画在平面直角坐标系中公通把数列的通项使用公式表示的方法式法项公式递推公式使用初始值a1和an+1=f(an)或a1,a2和an+1=f(an,an-1)等表示数列的方法知识点3an与Sn的关系若数列{an}的前n项和为Sn,通项公式为an,则an=知识点4等差数列1.定义:an+1-an=d(常数)(n∈N*).2.通项公式:an=a1+(n-1)d,an=am+(n-m)d.3.前n项和公式:Sn=na1+=.4.a,b的等差中项A=.5.等差数列的性质;(1)若m,n,p,q,k是正整数,且m+n=p+q=2k,则am+an=ap+aq=2ak.(2)am,am+k,am+2k,am+3k,…仍是等差数列,公差为kd.(3)若{an},{bn}是等差数列,则{pan+qbn}是等差数列.(4)数列Sm,S2m-Sm,S3m-S2m,…,也是等差数列.知识点5等比数列1.定义:如果一个数列从第2项起,每一项与它的前一项的比等于同一常数(不为零),那么这个数列就叫做等比数列.这个常数叫做等比数列的公比,通常用字母q表示,公比的表达式为=q.2.通项公式:an=a1qn-1=amqn-m.3.前n项和公式:Sn=4.等比中项G是a与b的等比中项⇔a,G,b成等比数列⇒G2=ab.5.等比数列的性质;(1)对任意的正整数m,n,p,q,若m+n=p+q=2k,则am·an=ap·aq=a.(2)若数列{an},{bn}(项数相同)是等比数列,则{λan},{|an|},,{a},{an·bn},(λ≠0)仍然是等比数列.(3)在等比数列{an}中,等距离取出若干项也构成一个等比数列,即an,an+k,an+2k,an+3k,…为等比数列,公比为qk.(4)公比不为-1的等比数列{an}的前n项和为Sn,则Sn,S2n-Sn,S3n-S2n仍成等比数列,其公比为qn,当公比为-1时,Sn,S2n-Sn,S3n-S2n不一定构成等比数列.专题一:数列的概念及表示【典例1】已知Sn为正项数列{an}的前n项和,且满足Sn=a+an(n∈N*).(1)求a1,a2,a3,a4的值;(2)求数列{an}的通项公式.【答案】(Ⅰ)见解析(Ⅱ)an=n.【举一反三】1.若数列{an}满足an+1=2an-1,且a8=16,则a6=________.【答案】【解析】 an+1=2an-1,∴a8=2a7-1=1...