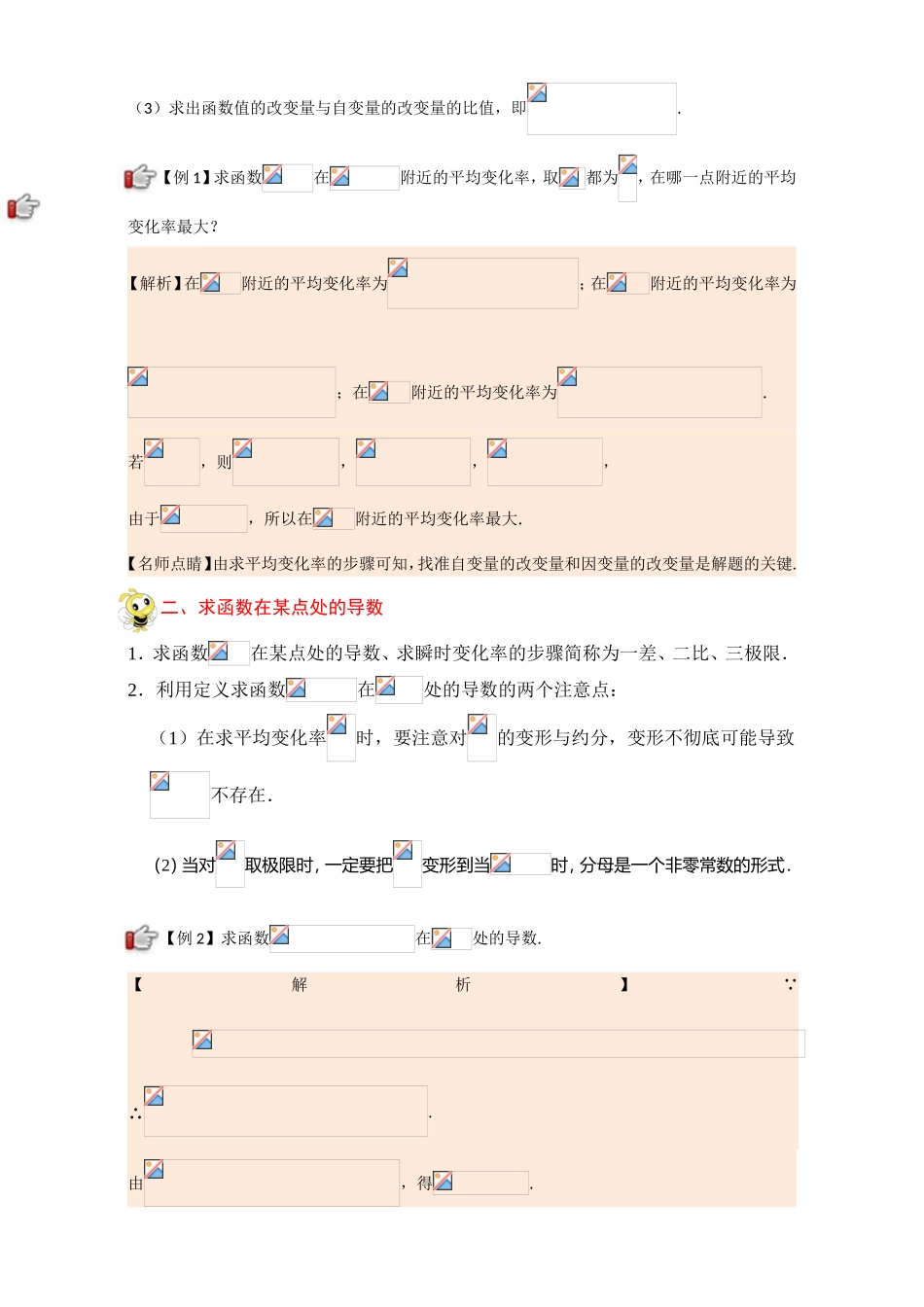
第三章导数及其应用3.1变化率与导数1.平均变化率设函数,我们把式子_________称为函数从到的平均变化率.习惯上用表示,即.函数的变化量是,于是,平均变化率可以表示为.其几何意义是函数图象上的两点所在直线的_________.注意:是一个整体符号,而不是与相乘.2.瞬时速度物体在不同时刻的速度是不同的,我们把物体在某一时刻的速度称为瞬时速度.设物体的运动规律为,则该物体在时刻的瞬时速度就是物体在到这段时间内,当无限趋近于0时,_____无限趋近的常数.3.导数的概念一般地,函数在处的瞬时变化率是,我们称它为函数在处的导数,记作_________,即.注意:不可以是0.4.导数的几何意义函数在处的导数,就是曲线在处的切线的_________,即.5.导函数对于函数,当时,是一个确定的数.这样,当变化时,_______便是一个关于的函数,我们称它为的导函数(简称导数).的导函数有时也记作______,即.注意:函数在处的导数与导函数是不同的,前者是一个数值,后者是一个函数,它们之间的关系是:函数在处的导数就是导函数在处的函数值.K知识参考答案:1.斜率2.3.或4.斜率5.K—重点平均变化率的概念、导数的概念、导数的几何意义、导函数K—难点导数的几何意义K—易错(1)运用定义求导数时容易忽略增量的一致性;(2)求切线方程时,错把所给点当做切点,或者混淆“某点处”和“过某点”一、求平均变化率求函数从到的平均变化率的三个步骤:(1)求出或者设出自变量的改变量:;(2)根据自变量的改变量求出函数值的改变量:;(3)求出函数值的改变量与自变量的改变量的比值,即.【例1】求函数在附近的平均变化率,取都为,在哪一点附近的平均变化率最大?【解析】在附近的平均变化率为;在附近的平均变化率为;在附近的平均变化率为.若,则,,,由于,所以在附近的平均变化率最大.【名师点睛】由求平均变化率的步骤可知,找准自变量的改变量和因变量的改变量是解题的关键.二、求函数在某点处的导数1.求函数在某点处的导数、求瞬时变化率的步骤简称为一差、二比、三极限.2.利用定义求函数在处的导数的两个注意点:(1)在求平均变化率时,要注意对的变形与约分,变形不彻底可能导致不存在.(2)当对取极限时,一定要把变形到当时,分母是一个非零常数的形式.【例2】求函数在处的导数.【解析】 ∴.由,得.【名师点睛】极限思想是趋近的思想,当平均变化率无限接近于瞬时变化率时,这个瞬时变化率就是平均变化率的极限.【例3】有一作直线运...