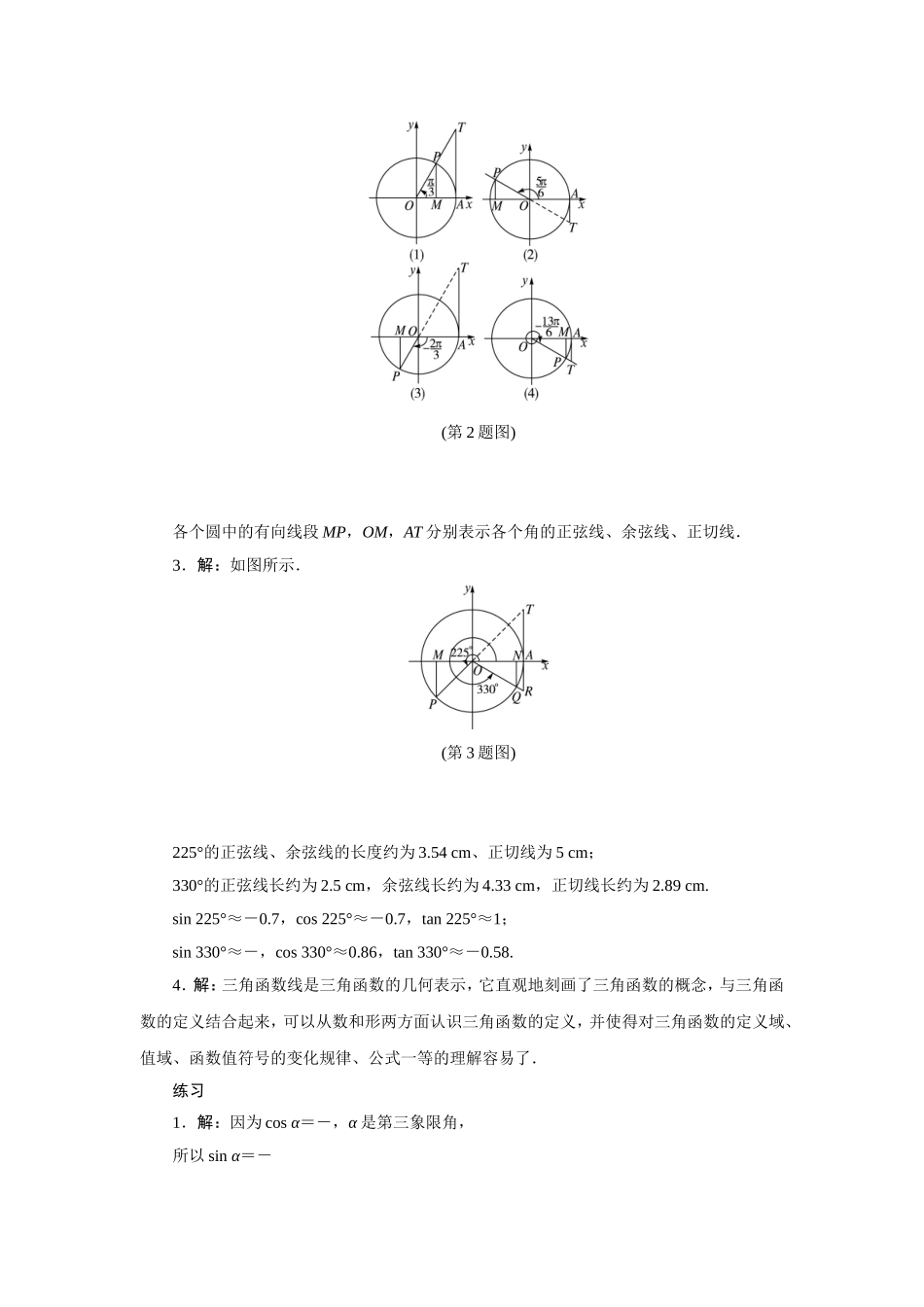
教材习题点拨练习11.解:sin=-,cos=-,tan=.点拨:根据定义求特殊角的三角函数值.2.解:r=|OP|==13,由三角函数的定义,可知sinθ=,cosθ=-,tanθ=-.3.解:角α0°90°180°270°360°角α的弧度数0π2πsinα010-10cosα10-101tanα0不存在0不存在04.解:当α是钝角时,cosα,tanα取负值.5.解:(1)正;(2)负;(3)零;(4)负;(5)正;(6)正.6.(1)①③或①⑤或③⑤;(2)①④或①⑥或④⑥;(3)②④或②⑤或④⑤;(4)②③或②⑥或③⑥.7.解:(1)0.8746;(2);(3);(4)1.练习21.解:终边相同的角的同一三角函数的值相等.2.解:如图所示.(第2题图)各个圆中的有向线段MP,OM,AT分别表示各个角的正弦线、余弦线、正切线.3.解:如图所示.(第3题图)225°的正弦线、余弦线的长度约为3.54cm、正切线为5cm;330°的正弦线长约为2.5cm,余弦线长约为4.33cm,正切线长约为2.89cm.sin225°≈-0.7,cos225°≈-0.7,tan225°≈1;sin330°≈-,cos330°≈0.86,tan330°≈-0.58.4.解:三角函数线是三角函数的几何表示,它直观地刻画了三角函数的概念,与三角函数的定义结合起来,可以从数和形两方面认识三角函数的定义,并使得对三角函数的定义域、值域、函数值符号的变化规律、公式一等的理解容易了.练习1.解:因为cosα=-,α是第三象限角,所以sinα=-=-=-,则tanα===.2.解:由可得或3.解:或4.解:(1)cosθtanθ=cosθ·=sinθ;(2)原式===1.5.证明:(1)左边=sin4α-cos4α=(sin2α+cos2α)(sin2α-cos2α)=sin2α-cos2α=右边,∴原命题成立;(2)左边=sin4α+sin2αcos2α+cos2α=sin2α(sin2α+cos2α)+cos2α=sin2α+cos2α=1=右边,∴原命题成立.习题1.2A组1.解:(1)sin=sin=sin=,cos=cos=cos=,tan=tan=tan=.(2)sin=sin=sin=-,cos=cos=cos=-,tan=tan=tan=1.(3)sin=sin=sin=,cos=cos=cos=,tan=tan=tan=.(4)sin1500°=sin(1440°+60°)=sin60°=,cos1500°=cos(1440°+60°)=cos60°=,tan1500°=tan(1440°+60°)=tan60°=.2.解:当a>0时,sinα=,cosα=,tanα=;当a<0时,sinα=-,cosα=-,tanα=.3.解:(1)-10;(2)15;(3)-;(4)-.点拨:直接代入各特殊角的三角函数值得解.4.解:(1)0;(2)(p-q)2;(3)(a-b)2;(4)0.5.解:(1)-2;(2)2.点拨:直接将x的具体数值代入函数f(x)的解析式,利用特...