2016-2017学年高中数学人教A版选修4-1章末综合测评2 Word版含解析.doc

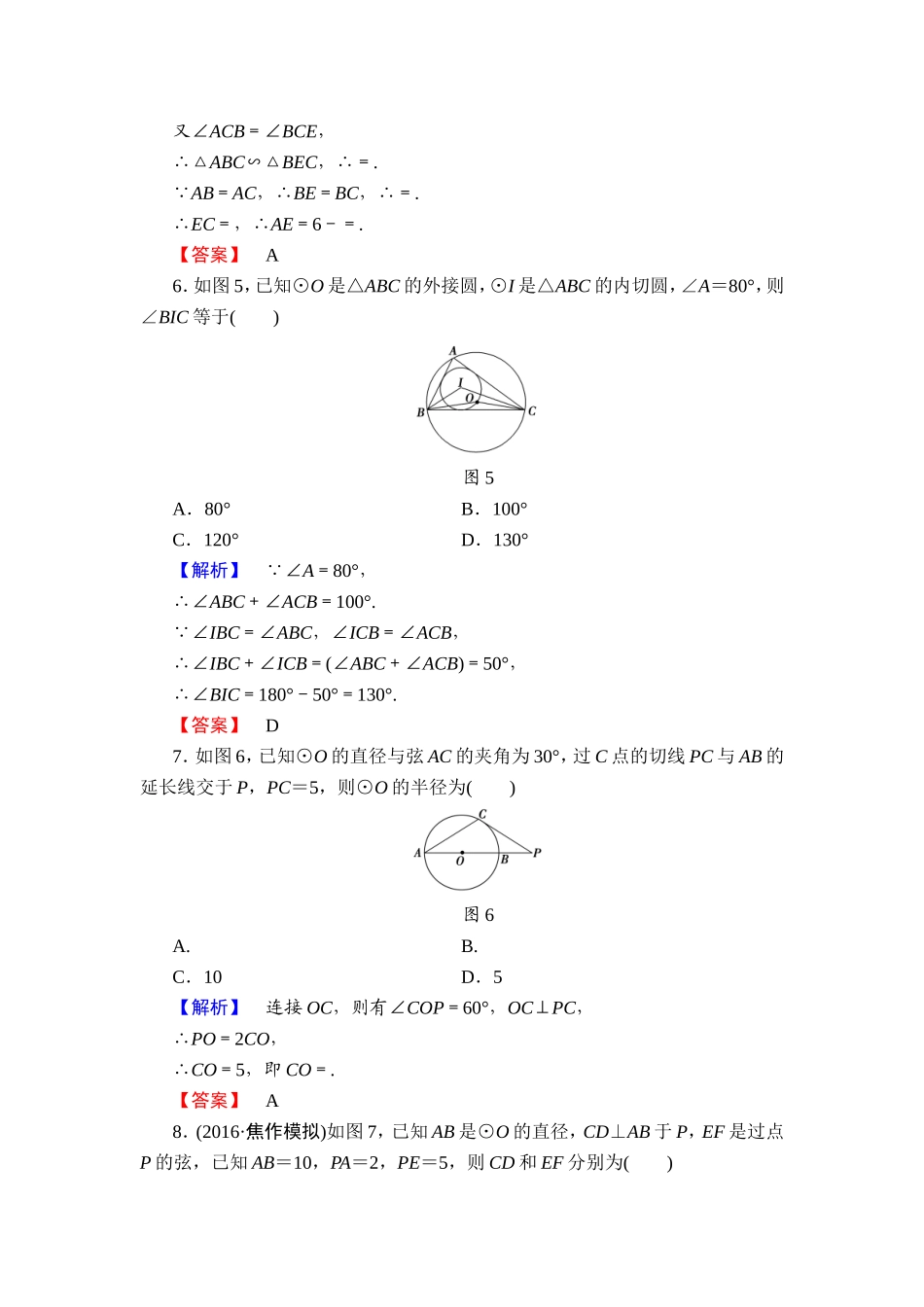
章末综合测评(二) (时间120分钟，满分150分) 一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的) 1．在⊙O中，∠AOB＝84°，则弦AB所对的圆周角是(　　) 【导学号：07370050】 A．42°　　　 B．138° C．84° D．42°或138° 【解析】　弦AB所对的弧的度数为84°或276°，故其所对的圆周角为42°或138°. 【答案】　D 2．如图1，一圆内切四边形ABCD，且AB＝16，CD＝10，则四边形的周长为(　　) 图1 A．50 B．52 C．54 D．56 【解析】　由切线长定理知CD＋AB＝AD＋BC. ∵AB＋CD＝26，∴AB＋BC＋CD＋AD＝52. 【答案】　B 3．如图2，⊙O经过⊙O1的圆心，∠ADB＝α，∠ACB＝β，则α与β之间的关系是(　　) 图2 A．β＝α B．β＝180°－2α C．β＝(90°－α) D．β＝(180°－α) 【解析】　如图所示，分别连接AO1，BO1. 根据圆内接四边形的性质定理，可得 ∠AO1B＋∠ADB＝180°， ∴∠AO1B＝180°－∠ADB＝180°－α. ∵∠ACB＝∠AO1B， ∴β＝(180°－α)，故选D. 【答案】　D 4.如图3所示，∠A＝50°，∠ABC＝60°，BD是⊙O的直径，则∠AEB等于 (　　) 图3 A．70° B．110° C．90° D．120° 【解析】　由题意知，∠D＝∠A＝50°， ∠BCD＝90°， ∴∠CBD＝90°－50°＝40°， 又∠ACB＝180°－50°－60°＝70°， ∴∠AEB＝∠CBD＋∠ACB＝40°＋70°＝110°. 【答案】　B 5．如图4，△ABC内接于⊙O，AB＝AC，直线MN切⊙O于点C，BE∥MN交AC于点E，若AB＝6，BC＝4，则AE＝(　　) 图4 A. B. C．1 D. 【解析】　∵MN为⊙O的切线，∴∠BCM＝∠A. ∵MN∥BE，∴∠BCM＝∠EBC， ∴∠A＝∠EBC. 又∠ACB＝∠BCE， ∴△ABC∽△BEC，∴＝. ∵AB＝AC，∴BE＝BC，∴＝. ∴EC＝，∴AE＝6－＝. 【答案】　A 6．如图5，已知⊙O是△ABC的外接圆，⊙I是△ABC的内切圆，∠A＝80°，则∠BIC等于(　　) 图5 A．80°　　 B．100° C．120° D．130° 【解析】　∵∠A＝80°， ∴∠ABC＋∠ACB＝100°. ∵∠IBC＝∠ABC，∠ICB＝∠ACB， ∴∠IBC＋∠ICB＝(∠ABC＋∠ACB)＝50°， ∴∠BIC＝180°－50°＝130°. 【答案】　D 7．如图6，已知⊙O的直径与弦AC的夹角为30°，过C点的切线PC与AB的延长线交于P，PC＝5，则⊙O的半径为(　　) 图6 A. B. C．10 D．5 【解析】　连接OC，则有∠COP＝60°，OC⊥PC， ∴PO＝2CO， ∴CO＝5，即CO＝. 【答案】　A 8．(2016·焦作模拟)如图7，已知AB是⊙O的直径，CD⊥AB于P，EF是过点P的弦，已知AB＝10，PA＝2，PE＝5，则CD和EF分别为(　　) 图7 A．8和7　　　 B．7和 C．7和8 D．8和 【解析】　∵PA·PB＝PC2， ∴PC2＝16，PC＝4，∴CD＝8. ∵PE·PF＝PC2，∴PF＝， ∴EF＝＋5＝. 【答案】　D 9．如图8，已知AT切⊙O于T.若AT＝6，AE＝3，AD＝4，DE＝2，则BC＝(　　) 图8 A．3 B．4 C．6 D．8 【解析】　∵AT为⊙O的切线， ∴AT2＝AD·AC. ∵AT＝6，AD＝4，∴AC＝9. ∵∠ADE＝∠B，∠EAD＝∠CAB， ∴△EAD∽△CAB， 即＝，∴BC＝＝＝6. 【答案】　C 10．如图9，圆内接△ABC的外角∠ACH的平分线与圆交于D点，DP⊥AC，垂足是P，DH⊥BH，垂足是H，下列结论：①CH＝CP；②＝；③AP＝BH；④DH为圆的切线．其中一定成立的是(　　) 图9 A．①②④ B．①③④ C．②③④ D．①②③ 【解析】　显然①可由△PCD≌△HCD得到；因为四边形ABCD为圆的内接四边形，所以∠BAD＝∠HCD＝∠ACD，即＝，故②成立；而③，连接BD，则AD＝BD，∠DAP＝∠DBH，所以Rt△APD≌Rt△BHD，得AP＝BH，③成立；对于④，不能判定DH是圆的切线，故应选D. 【答案】　D 11.如图10，在⊙O中，MN为直径，点A在⊙O上，且∠AON＝60°，点B是的中点，点P是直径MN上一动点，⊙O的半径为1，则AP＋BP的最小值为(　　) 图10 A．1 B. C.－1 D. 【解析】　如图，过点B作BB′⊥MN，交⊙O于点B′，连接AB′交MN于点P′，即点P在点P′处时，AP＋BP最小． 易知B与B′点关于MN对称， 依题意∠AON＝60°， 则∠B′ON＝∠BON＝30°， 所以∠AOB′＝90°， AB′＝＝. 故PA＋PB的最小值为，故选D. 【答案】　D 12．如图11所示，PT与⊙O切于T，CT是⊙O的直径，PBA是割线，与⊙O的交点是A，B，与直线CT的交点D，已知CD＝2，AD＝3，BD＝4，那么PB＝(　　) 图11 A．10 B．20 C．5 D．8 【解析】　根据相交弦定理，可得 AD·DB＝CD·DT，∴3×4＝2DT，解得DT＝6， ∴圆的半径r＝4，AB＝7，不妨设PB＝x，则PA＝x＋7，根据切割线定理，可得PT2＝PB·PA，∴PT2＝x·(x＋7)，在Rt△PTD中，DT2＋PT2＝PD2，∴36＋PT2＝(x＋4)2，∴36＋x(x＋7)＝(x＋4)2，解得x＝20. 【答案】　B 二、填空题(本大题共4小题，每小题5分，共20分，请把答案填在题中横线上) 13．如图12所示，在圆O中，直径AB与弦CD垂直，垂足为E，EF⊥DB，垂足为F，若AB＝6，AE＝1，则DF·DB＝________. 图12 【解析】　由题意知，AB＝6，AE＝1，∴BE＝5. ∴CE·DE＝DE2＝AE·BE＝5. 在Rt△DEB中，∵EF⊥DB，由射影定理得DF·DB＝DE2＝5. 【答案】　5 14．如图13，在半径为的⊙O中，弦AB，CD相交于点P，PA＝PB＝2，PD＝1，则圆心O到弦CD的距离为________． 图13 【解析】　由相交弦定理得PA·PB＝PC·PD. 又PA＝PB＝2，PD＝1，则PC＝4， ∴CD＝PC＋PD＝5. 过O作CD的垂线OE交CD于E，则E为CD中点， ∴OE＝＝＝. 【答案】　 15.如图14，△ABC为圆的内接三角形，BD为圆的弦，且BD∥AC.过点A作圆的切线与DB的延长线交于点E，AD与BC交于点F.若AB＝AC，AE＝6，BD＝5，则线段CF的长为________． 【导学号：07370051】 图14 【解析】　因为AB＝AC，所以∠ABC＝∠C.因为AE与圆相切，所以∠EAB＝∠C.所以∠ABC＝∠EAB，所以AE∥BC.又因为AC∥DE，所以四边形AEBC是平行四边形．由切割线定理可得AE2＝EB·ED，于是62＝EB·(EB＋5)，所以EB＝4(负值舍去)，因此AC＝4，BC＝6.又因为△AFC∽△DFB，所以＝，解得CF＝. 【答案】　 16．(2016·北京朝阳区检测)如图15，PC切圆O于点C，割线PAB经过圆心O，PC＝4，PB＝8，则tan∠COP＝________，△OBC的面积是________． 图15 【解析】　因为PC切圆O于点C，根据切割线定理即可得出PC2＝PA·PB，所以42＝8PA，解得PA＝2.设圆的半径为R，则2＋2R＝8，解得R＝3.在直角△OCP中，tan∠COP＝，sin∠COP＝.所以sin∠BOC＝sin∠COP＝.所以△OBC的面积是×R2sin∠BOC＝×32×＝. 【答案】　　 三、解答题(本大题共6小题，共70分．解答时应写出文字说明、证明过程或演算步骤) 17．(本小题满分10分)如图16，AB是⊙O的直径，弦BD，CA的延长线相交于点E，EF垂直BA的延长线于点F. 求证：(1)BE·DE＋AC·CE＝CE2； (2)E，F，C，B四点共圆． 图16 【证明】　(1)连接CD，由圆周角性质可知∠ECD＝∠EBA. 故△ABE∽△CDE，∴BE∶CE＝AE∶DE， ∴BE·DE＋AC·CE＝CE2. (2)∵AB是⊙O的直径，所以∠ECB＝90°，∴CD＝BE.∵EF⊥BF，∴FD＝BE，∴E，F，C，B四点与点D等距，∴E，F，C，B四点共圆． 18．(本小题满分12分)(2016·全国卷Ⅲ)如图17，⊙O中的中点为P，弦PC，PD分别交AB于E，F两点． 图17 (1)若∠PFB＝2∠PCD，求∠PCD的大小； (2)若EC的垂直平分线与FD的垂直平分线交于点G，证明：OG⊥CD. 【解】　(1)连接PB，BC，则∠BFD＝∠PBA＋∠BPD，∠PCD＝∠PCB＋∠BCD. 因为＝，所以∠PBA＝∠PCB.又∠BPD＝∠BCD， 所以∠BFD＝∠PCD. 又∠PFB＋∠BFD＝180°， ∠PFB＝2∠PCD， 所以3∠PCD＝180°，因此∠PCD＝60°. (2)证明：因为∠PCD＝∠BFD，所以∠EFD＋∠PCD＝180°，由此知C，D，F，E四点共圆，其圆心既在CE的垂直平分线上，又在DF的垂直平分线上，故G就是过C，D，F，E四点的圆的圆心，所以G在CD的垂直平分线上．又O也在CD的垂直平分线上，因此OG⊥CD. 19．(本小题满分12分)如图18，已知PE切⊙O于点E，割线PBA交⊙O于A，B两点，∠APE的平分线和AE，BE分别交于点C，D.求证： 图18 (1)CE＝DE； (2)＝. 【证明】　(1)∵PE切⊙O于点E，∴∠A＝∠BEP. ∵PC平分∠APE，∴∠A＋∠CPA＝∠BEP＋∠DPE. ∵∠ECD＝∠A＋∠CPA，∠EDC＝∠BEP＋∠DPE， ∴∠ECD＝∠EDC，∴CE＝DE. (2)∵∠PDB＝∠EDC，∠EDC＝∠ECD，∠PDB＝∠PCE， ∴∠BPD＝∠EPC，∴△PBD∽△PEC，∴＝. 同理△PDE∽△PCA，∴＝. ∴＝.∵DE＝CE，∴＝. 20．(本小题满分12分)如图19，D，E分别为△ABC边AB，AC的中点，直线DE交△ABC的外接圆于F，G两点．若CF∥AB，证明： 图19 (1)CD＝BC； (2)△BCD∽△GBD. 【证明】　(1)因为D，E分别为AB，AC的中点，所以DE∥BC.又已知CF∥AB，故四边形BCFD是平行四边形，所以CF＝BD＝AD.而CF∥AD，连接AF，所以四边形ADCF是平行四边形，故CD＝AF. 因为CF∥AB，所以BC＝AF，故CD＝BC. (2)因为FG∥BC，故GB＝CF. 由(1)可知BD＝CF，所以GB＝BD，所以∠BGD＝∠BDG. 由BC＝CD知∠CBD＝∠CD B. 又因为∠DGB＝∠EFC＝∠DBC，所以△BCD∽△GBD. 21．(本小题满分12分)(2016·全国卷Ⅰ)如图20，△OAB是等腰三角形，∠AOB＝120°，以O为圆心，OA为半径作圆． 图20 (1)证明：直线AB与⊙O相切； (2)点C，D在⊙O上，且A，B，C，D四点共圆，证明：AB∥CD. 【证明】　(1)设E是AB的中点，连接OE. 因为OA＝OB，∠AOB＝120°， 所以OE⊥AB，∠AOE＝60°. 在Rt△AOE中，OE＝AO，即O到直线AB的距离等于⊙O的半径，所以直线AB与⊙O相切． (2)因为OA＝2OD， 所以O不是A，B，C，D四点所在圆的圆心． 设O′是A，B，C，D四点所在圆的圆心，作直线OO′. 由已知得O在线段AB的垂直平分线上， 又O′在线段AB的垂直平分线上，所以OO′⊥A B. 同理可证，OO′⊥CD，所以AB∥CD. 22．(本小题满分12分)如图21，已知CP为⊙O的直径，AC切⊙O于点C，AB切⊙O于点D，并与CP的延长线相交于点B，又BD＝2BP. 图21 求证：(1)PC＝3BP； (2)AC＝PC. 【证明】　(1)∵BD是⊙O的切线， BPC是⊙O的割线， ∴BD2＝BP·BC. ∵BD＝2BP， ∴4BP2＝BP·BC， ∴4BP＝BC. ∵BC＝BP＋PC. ∴4BP＝BP＋PC， ∴PC＝3BP. (2)连接DO. ∵AB切⊙O于点D，AC切⊙O于点C， ∴∠ODB＝∠ACB＝90°. ∵∠B＝∠B，∴△ODB∽△ACB， ∴＝＝＝， ∴AC＝2DO，又PC＝2DO，∴AC＝PC.