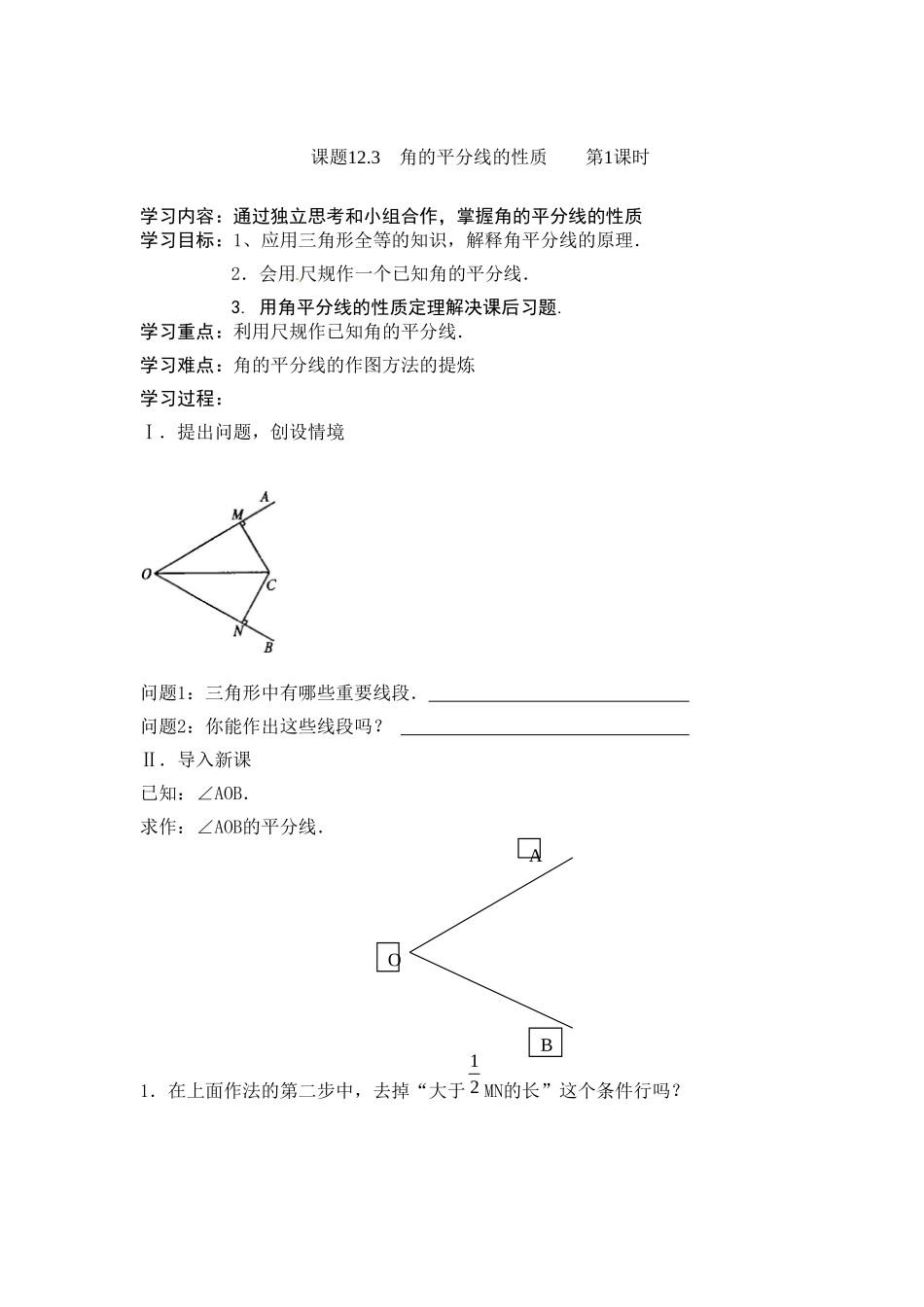
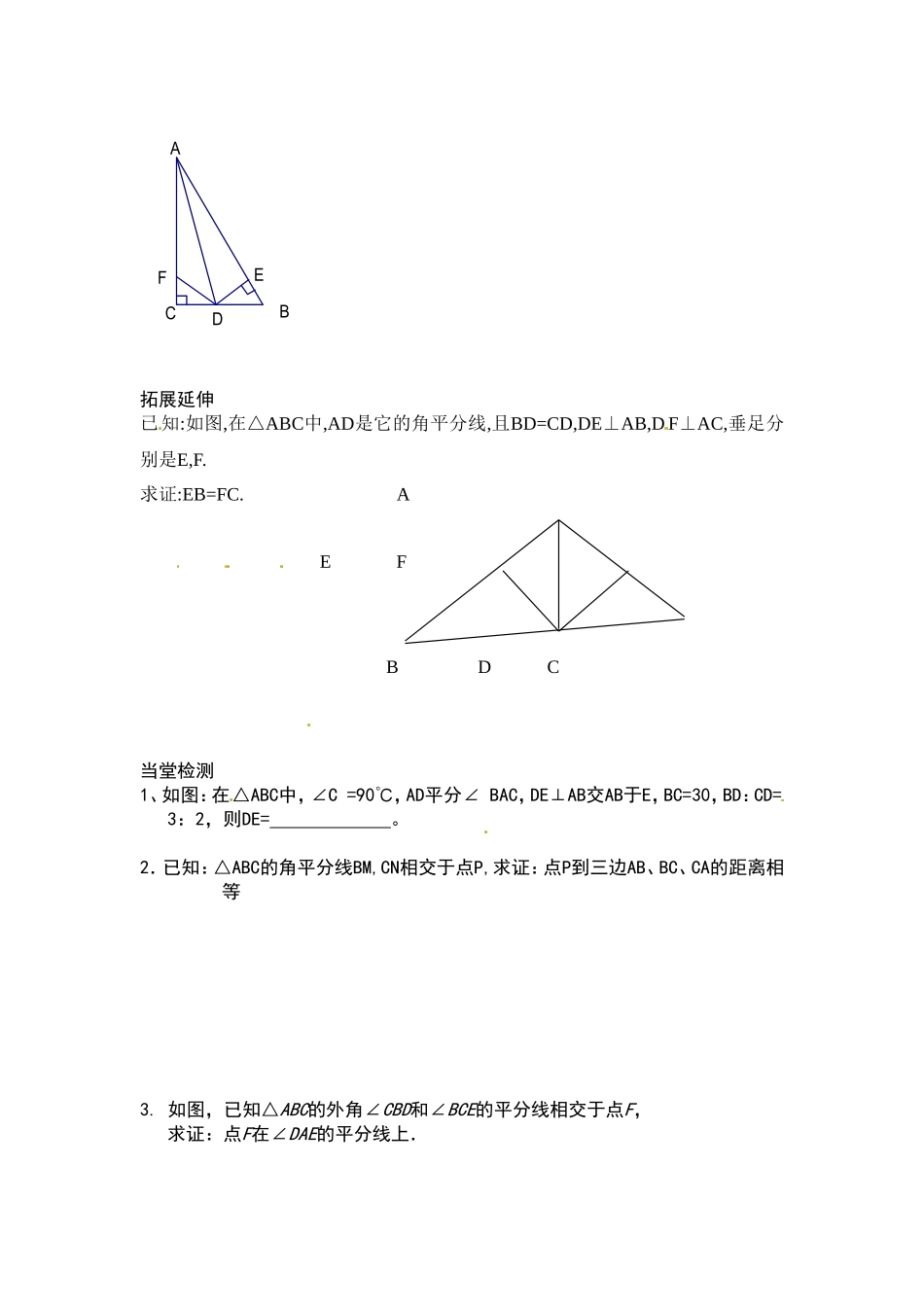
课题12.3角的平分线的性质第1课时学习内容:通过独立思考和小组合作,掌握角的平分线的性质学习目标:1、应用三角形全等的知识,解释角平分线的原理.2.会用尺规作一个已知角的平分线.3.用角平分线的性质定理解决课后习题.学习重点:利用尺规作已知角的平分线.学习难点:角的平分线的作图方法的提炼学习过程:Ⅰ.提出问题,创设情境问题1:三角形中有哪些重要线段.问题2:你能作出这些线段吗?Ⅱ.导入新课已知:∠AOB.求作:∠AOB的平分线.1.在上面作法的第二步中,去掉“大于12MN的长”这个条件行吗?AOB2.第二步中所作的两弧交点一定在∠AOB的内部吗?基础练习1.把一个平角三等分,则边上的两角的平分线的夹角是2.邻补角的平分线的夹角为3,已知点O是⊿ABC内的一点,且点O到三边的距离相等,则点O是()A,三条中线的交点B,三条高的交点C,三条角平分线的交点D,一条角平分线的中点4,⊿ABC中,∠C=90°,AD平分∠BAC交BC于D,BD:DC=3:2,点D到AB的距离为6,则BC等于()A,10B,20C,15D,255.如图,已知AO平分∠BAC,OE⊥AB,OD⊥AC。求证:OE=OD。课时小结巩固练习:已知:如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上BD=DF,求证:CF=EB。DFECBA拓展延伸已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:EB=FC.AEFBDC当堂检测1、如图:在△ABC中,∠C=90℃,AD平分∠BAC,DE⊥AB交AB于E,BC=30,BD:CD=3:2,则DE=。2.已知:△ABC的角平分线BM,CN相交于点P,求证:点P到三边AB、BC、CA的距离相等3.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上.4.已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD课后反思:EDCAB