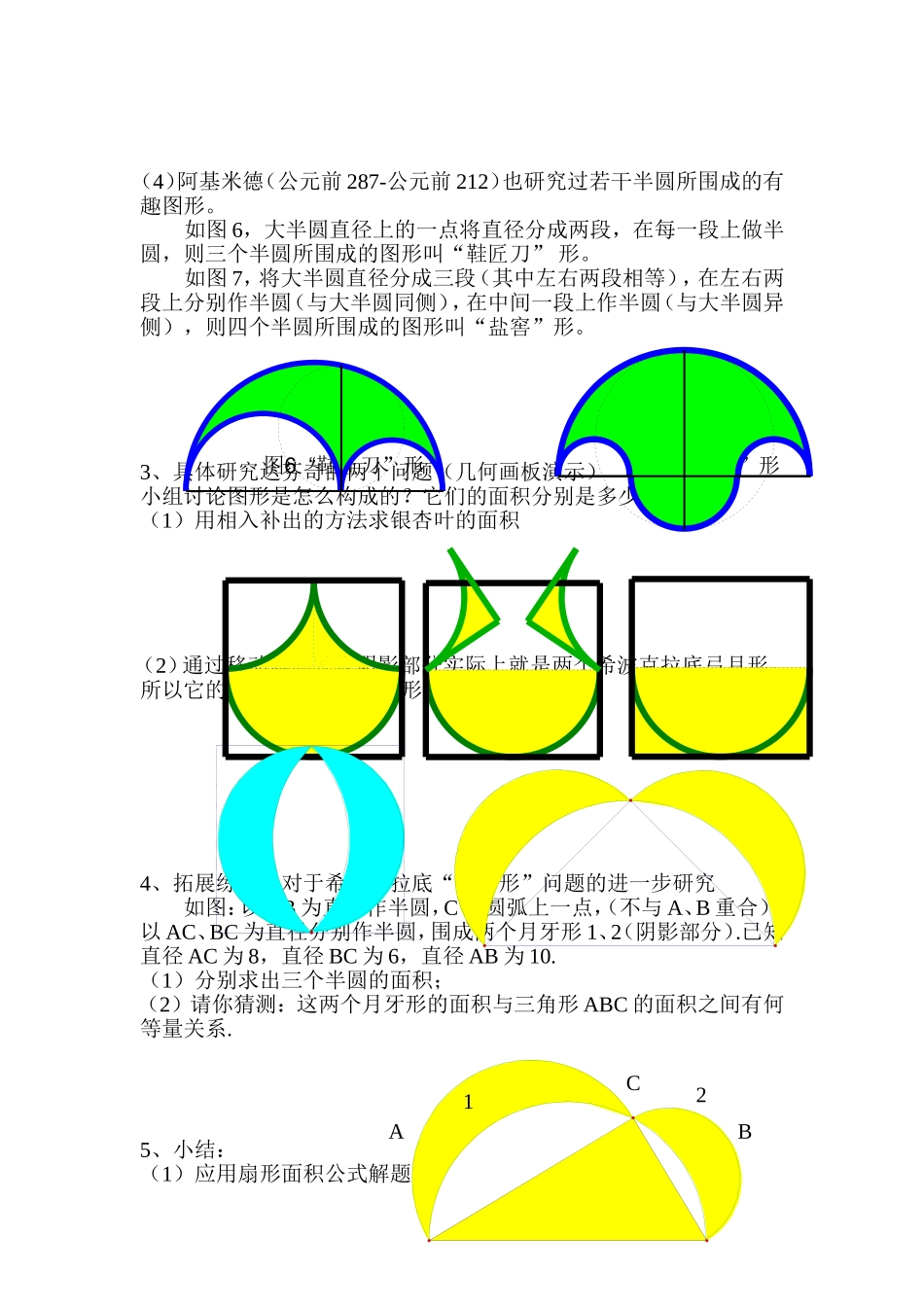
扇形的面积(2)教学设计一、教学内容:数学六年级第一学期第四章第四节上海教育出版社二、教材分析:教材的地位和作用扇形的面积第二课时是六年级第一学期的最后一节课时,是对扇形面积公式的具体应用。这个知识点在初中数学新课程中是作为“圆中的计算问题”出现的。通过对复杂图形的研究让学生为进一步学习圆里面的内容打下坚实基础。三、学情分析:在此之前,学生已经初步认识了圆,知道圆的周长公式、面积公式,以及弧长公式和扇形面积公式,为学生研究复杂图形的面积做好了知识迁移基础。学好这部分内容,不仅可以从形的方面加深对周围事物的理解,发展学生的空间观念,可以在探索实验和联系生活应用数学方面拓展学生的知识面,发展学生的思维和解决实际问题的能力,同时也为学习其他平面图形和立体图形积累知识经验,为进一步学习圆里面的内容打下坚实基础。四、教学目标:1、能用公式进行有关的面积计算2、理解复杂图形是由基本图形组合而成的3、通过对数学史上有关扇形问题的解决体会数学的博大精深五、教学重点与难点:扇形面积公式的应用。六、教学环节1、引入:展示意大利艺术大师达芬奇(1452~1519)的素描头像,提问:达芬奇给你的印象是什么呢?(学生有可能会回答有关蒙娜丽莎或者画鸡蛋的故事)事实上,达芬奇对数学也很有研究:比如对银杏叶和猫眼的研究这是由两段四分之一圆弧与一段半圆所围成的图形2、追述古人对圆弧的研究(1)大英博物馆所藏古巴比伦时期(公元前1800年-公元前1600年)的数学泥版BM15285。可以看到很多求圆弧或圆弧与线段所围成的一些有趣图形的面积问题,如图1~图3所示。这些问题很可能就是当时的数学练习题。(2)古代两河流域的陶碗以及中国仰韶文化陶盆上的花瓣纹则表明,新石器时代的人们已经知道用圆弧来构造若干对称图形了。(3)古希腊数学家希波克拉底(公元前5世纪)研究化圆为方的问题时,求得了某些特殊的弓月形面积,与扇形面积密切相关。在图4中,希波克拉底发现,等腰直角三角形斜边上的半圆与以直角顶点为圆心、直角边为半径的四分之一圆弧所围成的弓月形面积与等腰直角三角形的面积相等。在图5中,希波克拉底发现,大圆内接正六边形相邻三边上的半圆与大圆所围成的三个弓月形连同其中一个小半圆的面积与等腰梯形面积相等。图4弓月形图5弓月形与等腰梯形(4)阿基米德(公元前287-公元前212)也研究过若干半圆所围成的有趣图形。如图6,大半圆直径上的一点将直径分成两段,在每一段上做半圆...