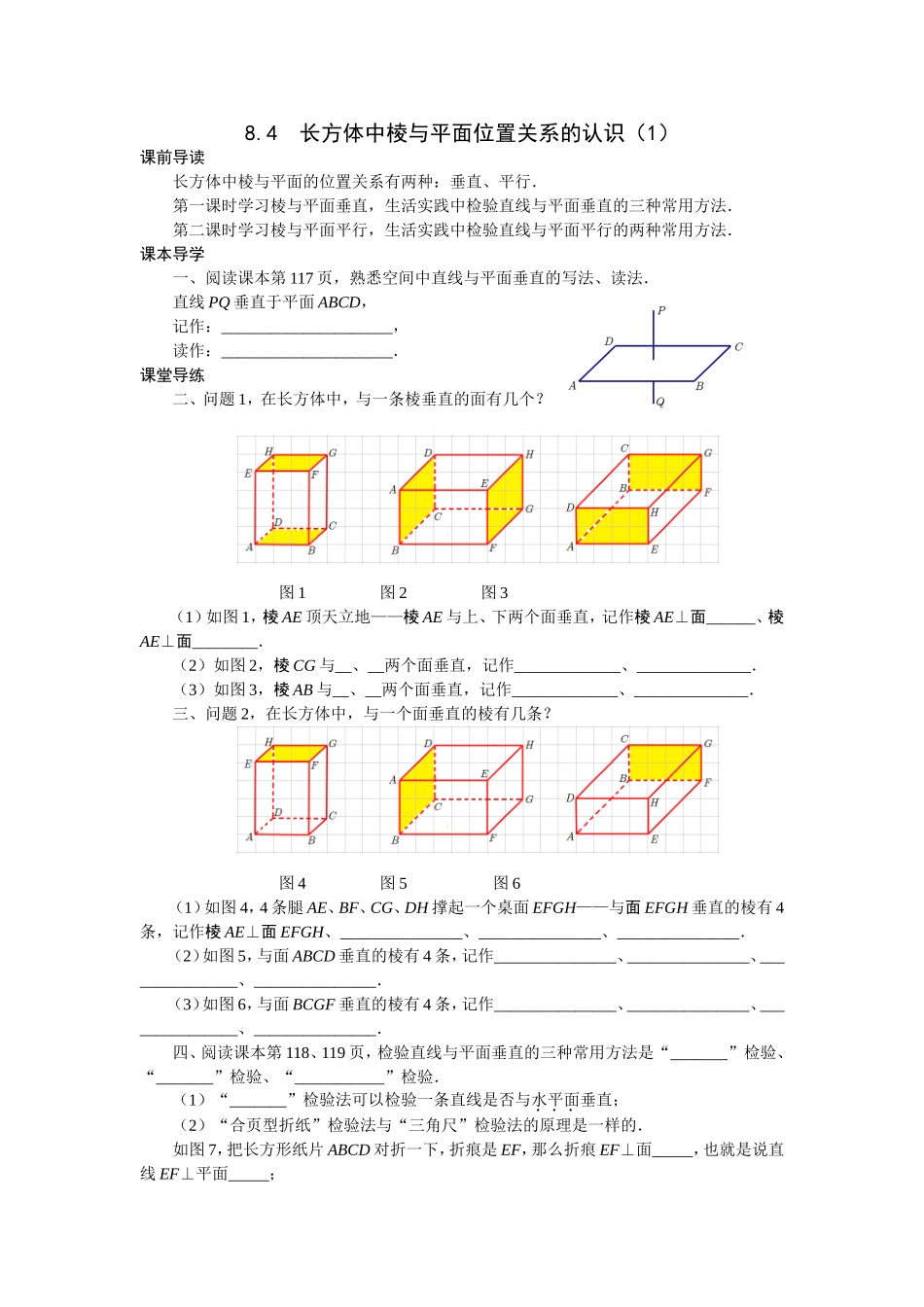
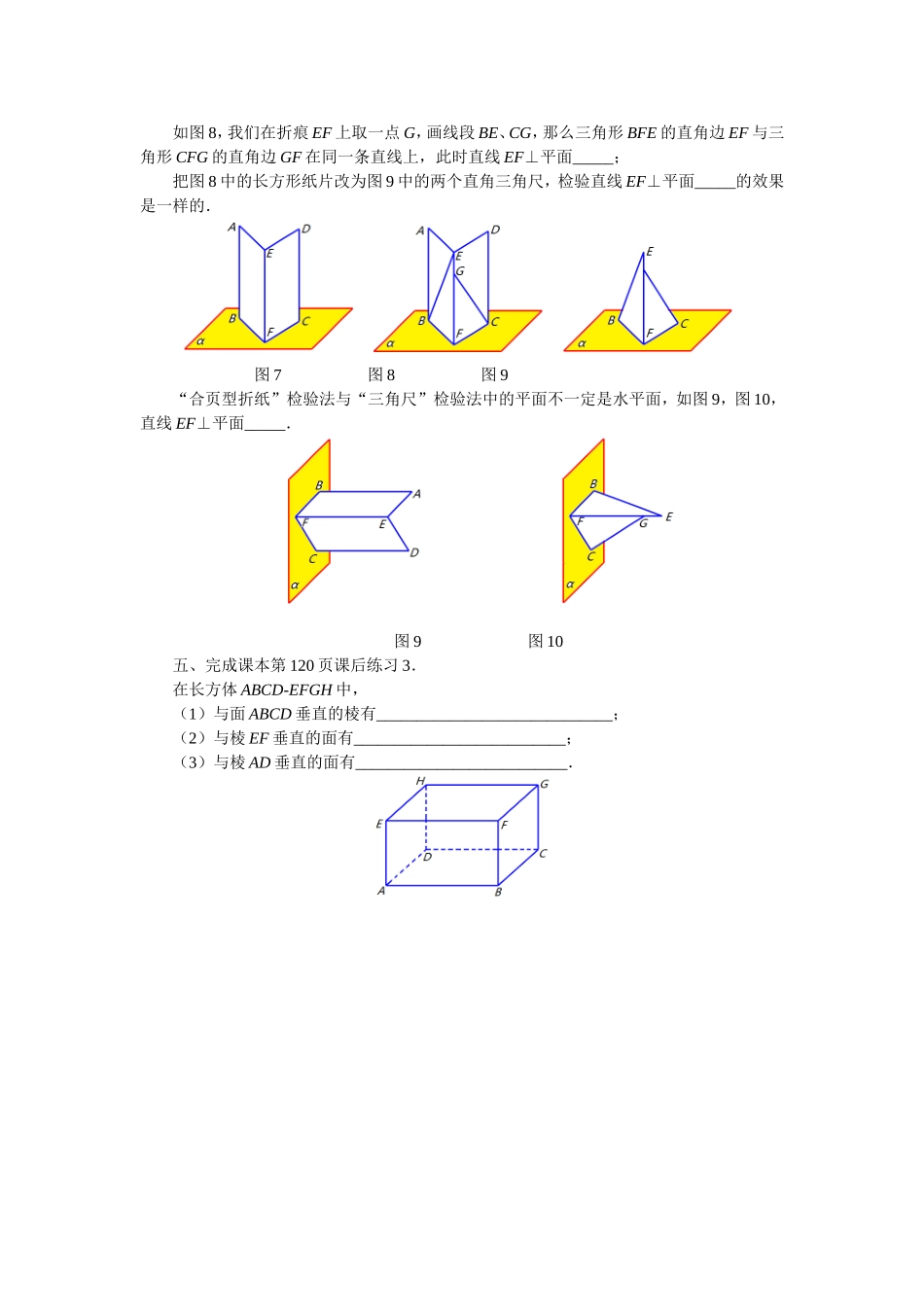
8.4长方体中棱与平面位置关系的认识(1)课前导读长方体中棱与平面的位置关系有两种:垂直、平行.第一课时学习棱与平面垂直,生活实践中检验直线与平面垂直的三种常用方法.第二课时学习棱与平面平行,生活实践中检验直线与平面平行的两种常用方法.课本导学一、阅读课本第117页,熟悉空间中直线与平面垂直的写法、读法.直线PQ垂直于平面ABCD,记作:_____________________,读作:_____________________.课堂导练二、问题1,在长方体中,与一条棱垂直的面有几个?图1图2图3(1)如图1,棱AE顶天立地——棱AE与上、下两个面垂直,记作棱AE⊥面______、棱AE⊥面________.(2)如图2,棱CG与__、__两个面垂直,记作_____________、______________.(3)如图3,棱AB与__、__两个面垂直,记作_____________、______________.三、问题2,在长方体中,与一个面垂直的棱有几条?图4图5图6(1)如图4,4条腿AE、BF、CG、DH撑起一个桌面EFGH——与面EFGH垂直的棱有4条,记作棱AE⊥面EFGH、_______________、_______________、_______________.(2)如图5,与面ABCD垂直的棱有4条,记作_______________、_______________、_______________、_______________.(3)如图6,与面BCGF垂直的棱有4条,记作_______________、_______________、_______________、_______________.四、阅读课本第118、119页,检验直线与平面垂直的三种常用方法是“_______”检验、“_______”检验、“___________”检验.(1)“_______”检验法可以检验一条直线是否与水平面垂直;(2)“合页型折纸”检验法与“三角尺”检验法的原理是一样的.如图7,把长方形纸片ABCD对折一下,折痕是EF,那么折痕EF⊥面_____,也就是说直线EF⊥平面_____;如图8,我们在折痕EF上取一点G,画线段BE、CG,那么三角形BFE的直角边EF与三角形CFG的直角边GF在同一条直线上,此时直线EF⊥平面_____;把图8中的长方形纸片改为图9中的两个直角三角尺,检验直线EF⊥平面_____的效果是一样的.图7图8图9“合页型折纸”检验法与“三角尺”检验法中的平面不一定是水平面,如图9,图10,直线EF⊥平面_____.图9图10五、完成课本第120页课后练习3.在长方体ABCD-EFGH中,(1)与面ABCD垂直的棱有_____________________________;(2)与棱EF垂直的面有__________________________;(3)与棱AD垂直的面有__________________________.8.4长方体中棱与平面位置关系的认识(2)课前导读第二课时学习棱与平...