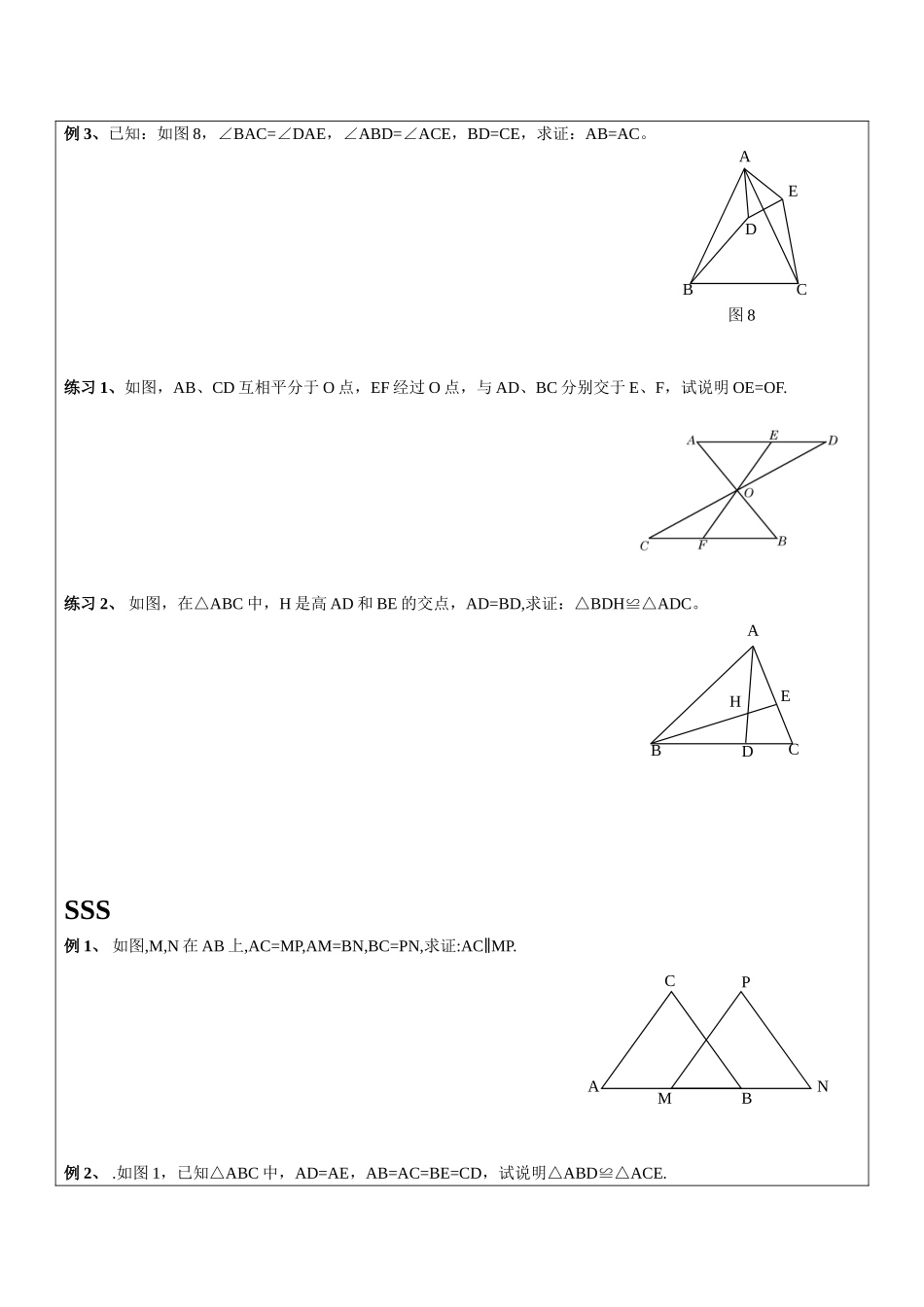
课题全等三角形判定教学目标1.掌握四种证明全等的方法;2.学习分析问题,处理一些特殊条件的技巧;3.能够快速准确找出适合题意的三角形全等的判定方法;重点、难点重点:能够快速准确找出适合题意的三角形全等的判定方法难点:学习分析证明命题的方法,培养分析能力考点及考试要求全等三角形的概念与性质的理解与应用教学内容一、知识点梳理三角形全等的判定判定方法1:判定方法2:判定方法3:判定方法4:二、例题讲解SAS例1、如图,已知等腰△ABC与△ADE中,AB=AC,AD=AE,且BAC=DAE,试说明△ABDACE.≌△例2、如图,△ABC和△CDE为等边三角形,B、C、E在同一直线上。求证:AE=BD;EABCMQPD练习1、如图,BF=DE,AE=CF,BFDE∥,试说明B=D.练习2、如图,△ABC,△BDF为等腰直角三角形,求证:(1)CF=AD;(2)CE⊥AD。ASA和AAS例1、如图,AB、CD相交于点O,△ACOBDO≌△,CEDF∥,求证:CE=DF.例2、如图,已知BE、CD相交于点O,B=C,1=2,试说明△AODAOE≌△CABDEFOACBDEF例3、已知:如图8,∠BAC=∠DAE,∠ABD=∠ACE,BD=CE,求证:AB=AC。练习1、如图,AB、CD互相平分于O点,EF经过O点,与AD、BC分别交于E、F,试说明OE=OF.练习2、如图,在△ABC中,H是高AD和BE的交点,AD=BD,求证:△BDHADC≌△。SSS例1、如图,M,N在AB上,AC=MP,AM=BN,BC=PN,求证:ACMP.∥例2、.如图1,已知△ABC中,AD=AE,AB=AC=BE=CD,试说明△ABDACE.≌△ABCPMNDAEBC图8ABDCHE课堂练习:1.在下列推理中填写需要补充的条件,使结论成立,如图,在中.≌(SAS)∴≌(ASA)∴≌(AAS)2、如图,AB=DB,,请你添加一个条件,使≌,则需添加的条件是什么?并说明理由.3、如图,D是中BC边上的一点E是AD上一点,EB=EC,,求证:.ABDECAO=DO(已知)=()=(已知)①②=(已知)AO=DO(已知)=()=()=(已知)AO=DO(已知)③ABCDOABCD12E家庭作业1.以下四个命题中,正确的是()A.有三个角对应相等的两个三角形全等B.有两边对应相等的两个三角形全等C.有一个角相等,并且有两条对应边相等的两个三角形全等D.有一边相等的两个等边三角形全等2.如图1,AM平分∠BAC,AD=AE,则此图中共有多少对全等三角形()A.1B.2C.3D.43.如图2,△ABC,△DCE都是等边三角形,且共点于C,则△DBC≌△EAC的依据是()A.边边边B.边边角C.边角边D.角边角4.在△ABC和△A′B′C′中,如果AB=A′B′,∠B=∠B′,AC=A′C′,那么这两个三角形()A.全等B.不一定全等C.不全等D.面积相...