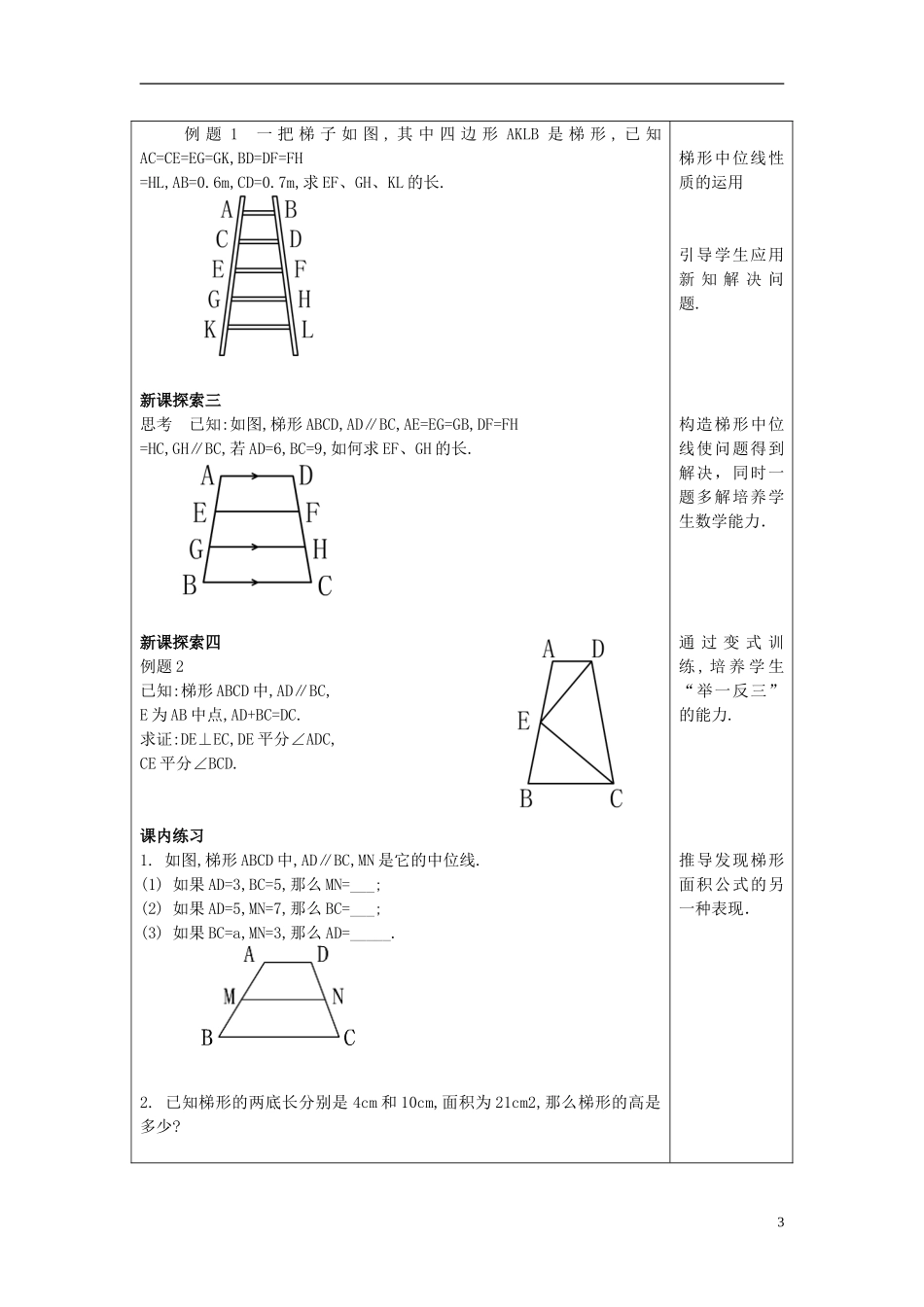
三角形、梯形的中位线课题22.6(2)三角形、梯形的中位线设计依据(注:只在开始新章节教学课必填)教材章节分析:学生学情分析:课型新授课教学目标1、掌握梯形中位线的概念和梯形中位线性质;2、能正确运用性质解决问题3、经历“操作→观察→猜想→验证”的探索过程;4、从图形运动的角度比较三角形中位线与梯形中位线培养积极探究的态度及合作交流意识.重点掌握梯形中位线的概念和梯形中位线性质.难点梯形中位线性质的证明.教学准备三角形中位线.学生活动形式讨论,交流,总结,练习教学过程设计意图课题引入:课前练习一1.填空:(1)顺次联结四边形各边中点得到的四边形一定是_______;(2)顺次联结对角线相等的四边形各边中点得到的四边形一定是_____(选填:矩形、菱形、正方形);(3)顺次联结对角线_________的四边形各边中点得到的四边形一定是矩形.课前练习二2.已知:如图,四边形ABCD中,AB=CD,M、P、N分别是AD、BD、BC的中点.求证:∠PMN=∠PNM.观察图形的变换介绍梯形的中位线。知识呈现:1猜想梯形中位线的性质。能证明你猜想的正确性吗?让学生有一个“操作→猜想→验证”的学习经历;总结梯形中位线定理并规范符号表达式。通过老师引领,使学生有一个规范符号表达式的过程.新课探索一(1)操作如图(1),D、E分别是△ABC的边AB,AC的中点(则DE与BC在位置上、数量上分别有什么关系?),过点A作∥BC,将AC所在直线绕点E旋转,交于点G,交BC于点F.观察(1)在上述运动过程中,四边形ABFG是一个什么图形?(2)点E是GF的哪一点?四边形ABFG(在一般情况下)是一个梯形(在特殊情况下是平行四边形),点E是GF的中点.联结梯形两腰中点的线段叫做梯形的中位线.如图(2)中,D、E分别是梯形两腰的中点,线段DE是梯形ABFG的中位线.猜想梯形的中位线与两底在位置上,数量上分别有什么关系?新课探索一(2)已知:如图,梯形ABFG中,AG∥BF,AD=DB,GE=EF.求证:DE∥BF,且DE=(BF+AG).新课探索一(3)梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半.符号表达式:在梯形ABCD中,AD∥BC,EF是梯形的中位线(AE=EB,DF=FC),∴EF∥BC∥AD,EF=(BC+AD).新课探索二2例题1一把梯子如图,其中四边形AKLB是梯形,已知AC=CE=EG=GK,BD=DF=FH=HL,AB=0.6m,CD=0.7m,求EF、GH、KL的长.新课探索三思考已知:如图,梯形ABCD,AD∥BC,AE=EG=GB,DF=FH=HC,GH∥BC,若AD=6,BC=9,如何求EF、GH的长.新课探索四例题2已知:梯形ABCD中,AD∥BC,E为AB中点,AD+BC=DC.求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.课内练习1.如...