八年级上册数学苏科第3章勾股定理知识点总结课件pptx_8.pptxVIP免费

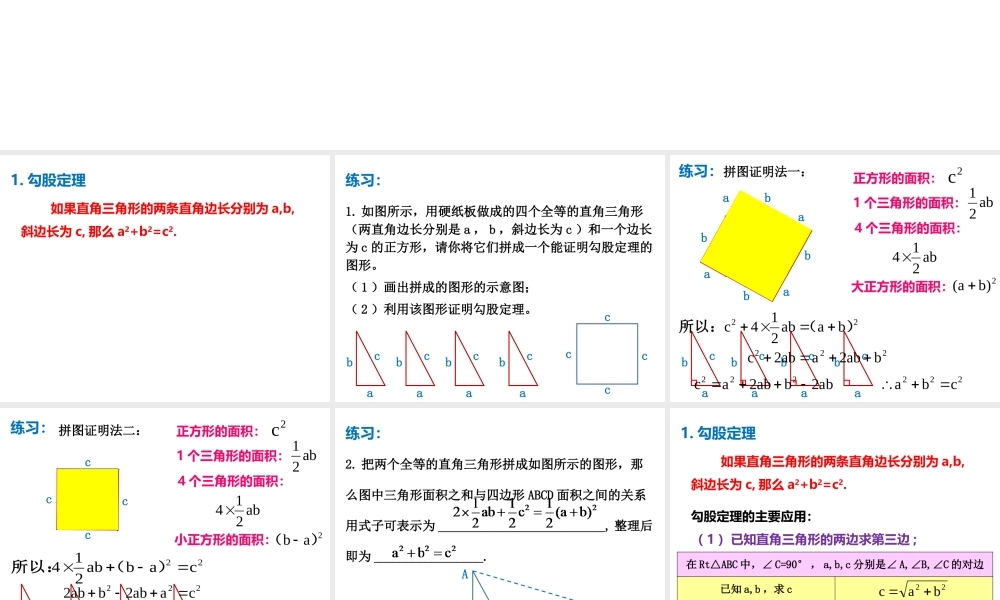
第3章勾股定理知识点总结1.勾股定理如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.练习：1.如图所示，用硬纸板做成的四个全等的直角三角形（两直角边长分别是a，b，斜边长为c）和一个边长为c的正方形，请你将它们拼成一个能证明勾股定理的图形。（1）画出拼成的图形的示意图；（2）利用该图形证明勾股定理。cabcabcabcccccab练习：拼图证明法一：cccc正方形的面积：cabcabcabcababbaabba2c1个三角形的面积：ab214个三角形的面积：ab214大正方形的面积：22baab214c）（所以：ab2c222bab2aab2bab2ac222222cba2)ba(练习：拼图证明法二：cccc正方形的面积：cabcabcabcab2c1个三角形的面积：ab214个三角形的面积：ab214小正方形的面积：222cba2ab）（22cabab214）（所以：222caab2bab2练习：2.把两个全等的直角三角形拼成如图所示的图形，那么图中三角形面积之和与四边形ABCD面积之间的关系用式子可表示为__________________________,整理后即为_________________.ABCDEaabbcc1.勾股定理如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.勾股定理的主要应用：（1）已知直角三角形的两边求第三边;在Rt△ABC中，∠C=90°，a,b,c分别是∠A,∠B,∠C的对边已知a,b，求c已知a,c，求b已知b,c，求a22bac22acb22bca练习：1.在△ABC中，∠C=90°，∠A、∠B、∠C的对边分别为a、b、c.（1）当a=3,b=4时，c=____________；（2）当AB=10,BC=8时，AC=____________.2.如图，直角三角形中未知边x=______,y=______.x1582425y561771.勾股定理如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.勾股定理的主要应用：（2）已知直角三角形的一边与另两边的关系，求直角三角形的另两边;练习：1.若一个直角三角形的一条直角边长是7cm，另一条直角边比斜边短1cm，则斜边的长是_______cm.2.直角三角形的斜边比一直角边长2cm，另一直角边长为6cm，则它的斜边长为（）A.2cmB.6cmC.8cmD.10cm3.已知直角三角形中，30°角所对的直角边长是cm，则另一条直角边的长是（）A.4cmB.cmC.6cmD.cm32343625DC1.勾股定理如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.勾股定理的主要应用：（3）利用勾股定理可以证明线段平方关系的问题.练习：1.如图，已知△ABC中，∠ACB=90°，以△ABC的各边为边在△ABC外作三个正方形，S1、S2、S3分别表示这三个正方形...