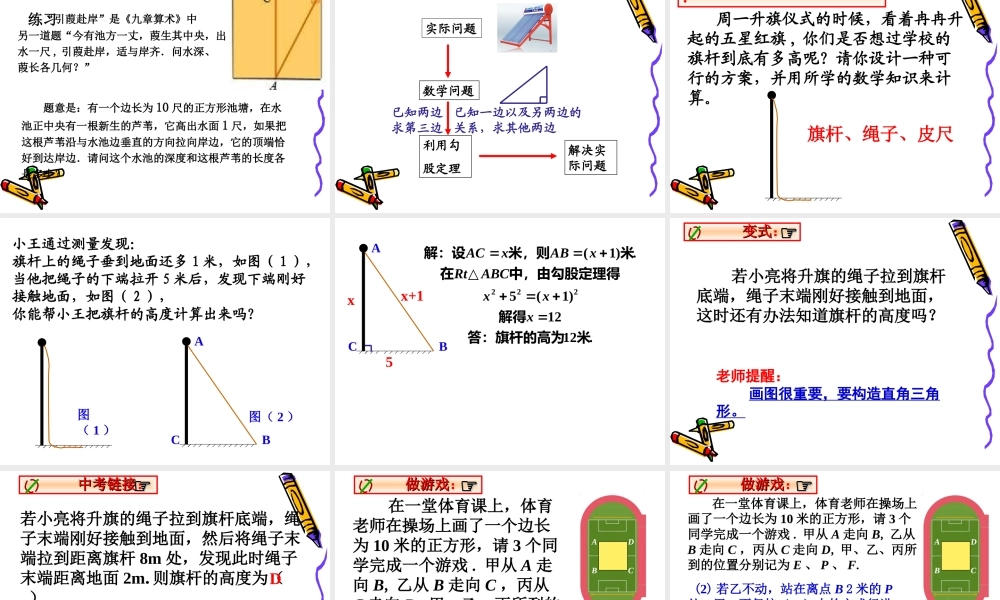
苏科版八年级数学上册学习目标:•1.能运用勾股定理及直角三角形的判定条件解决实际问题;•2.构造直角三角形及正确解出此类方程;•3.运用勾股定理解释生活中的实际问题.勾股定理(gou-gutheorem)如果直角三角形两直角边分别为a、b,斜边为c,那么222abc即直角三角形直角三角形两直角边的平方和等于斜边的平方。abc知识回顾BC如图,太阳能热水器的支架AB长为90cm,与AB垂直的BC长为120cm.太阳能真空管AC有多长?[来源:Zxxk.Com]ABC90cm120cm?实际问题数学问题利用勾股定理已知两边求第三边解决实际问题数学思想,建模思想数学思想,建模思想☞☞我爱我校我爱我校:☞☞如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,仅仅少走了________步路,却踩伤了花草。(假设1米为2步)如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,仅仅少走了________步路,却踩伤了花草。(假设1米为2步)我爱我校我爱我校:☞☞如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,仅仅少走了________步路,却踩伤了花草。(假设1米为2步)3米4米“路”ABC5米4我爱我校我爱我校:☞☞例1九章算术中的“折竹”问题:今有竹高一丈,末折抵地,去根三尺,问折者高几何?意思是:有一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?3.3勾股定理的简单应用3.3勾股定理的简单应用解:如图,我们用线段OA和线段AB来表示竹子,其中线段AB表示竹子折断部分,用线段OB来表示竹梢触地处离竹根的距离.设OA=x,则AB=10-x. ∠AOB=90°,∴OA2+OB2=AB2,∴x2+32=(10-x)2.AOBX(10-X)33.3勾股定理的简单应用3.3勾股定理的简单应用.0.5xx+0.52校园生活中的数学校园生活中的数学:☞☞荷花问题平平湖水清可鉴,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边;渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅.校园生活中的数学校园生活中的数学:☞☞荷花问题平平湖水清可鉴,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边;渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅.B校园生活中的数学校园生活中的数学:☞☞练习“引葭赴岸”是《九章算术》中另一道题“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”题意是:有一个边长...