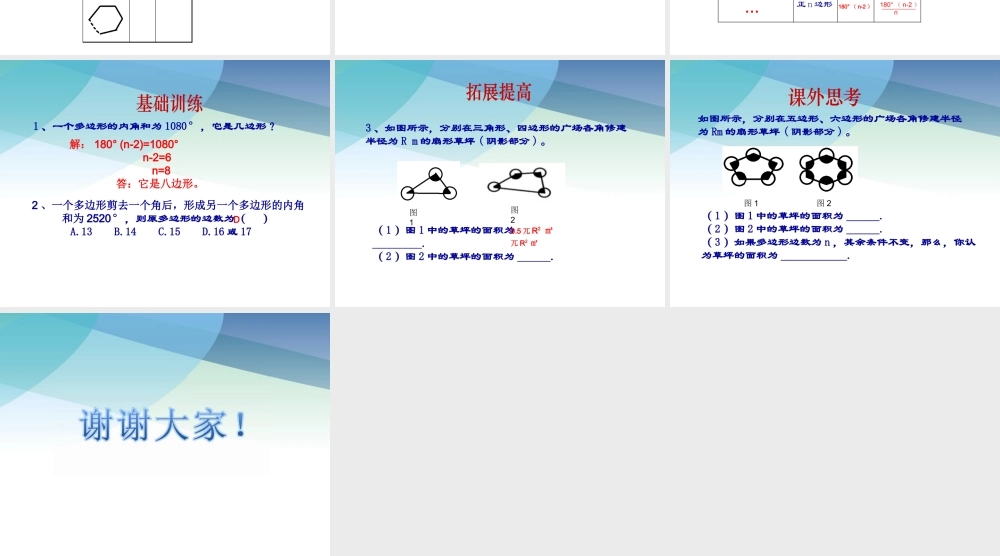
22.7多边形的内角和与外角和1.经历探究多边形内角和公式的过程,进一步发展合情推理能力。2.掌握多边形的内角和公式,进一步发展演绎推理能力。(1)三角形的内角和等于______。(2)长方形的内角和等于______,(3)正方形的内角和等于______。180°360°360°(1)议一议探究任意四边形的内角和,并说说你的方法。从同一个顶点引对角线,五边形、六边形分别可以分成多少个三角形?n边形呢?多边形三角形内角和(2)找一找n边形的内角和等于180°(n-2)内角和定理你能求出下列正多边形的每个内角吗?图形正多边形内角和每个内角正三角形正四边形正五边形正六边形正n边形…(3)想一想180°180°(n-2)360°540°720°90°60°120°108°180°(n-2)n1、一个多边形的内角和为1080°,它是几边形?解:180°(n-2)=1080°n-2=6n=8答:它是八边形。2、一个多边形剪去一个角后,形成另一个多边形的内角和为2520°,则原多边形的边数为()A.13B.14C.15D.16或17D3、如图所示,分别在三角形、四边形的广场各角修建半径为Rm的扇形草坪(阴影部分)。(1)图1中的草坪的面积为_________.(2)图2中的草坪的面积为______.图10.5兀R2㎡兀R2㎡图2如图所示,分别在五边形、六边形的广场各角修建半径为Rm的扇形草坪(阴影部分)。(1)图1中的草坪的面积为______.(2)图2中的草坪的面积为______.(3)如果多边形边数为n,其余条件不变,那么,你认为草坪的面积为____________.图1图2