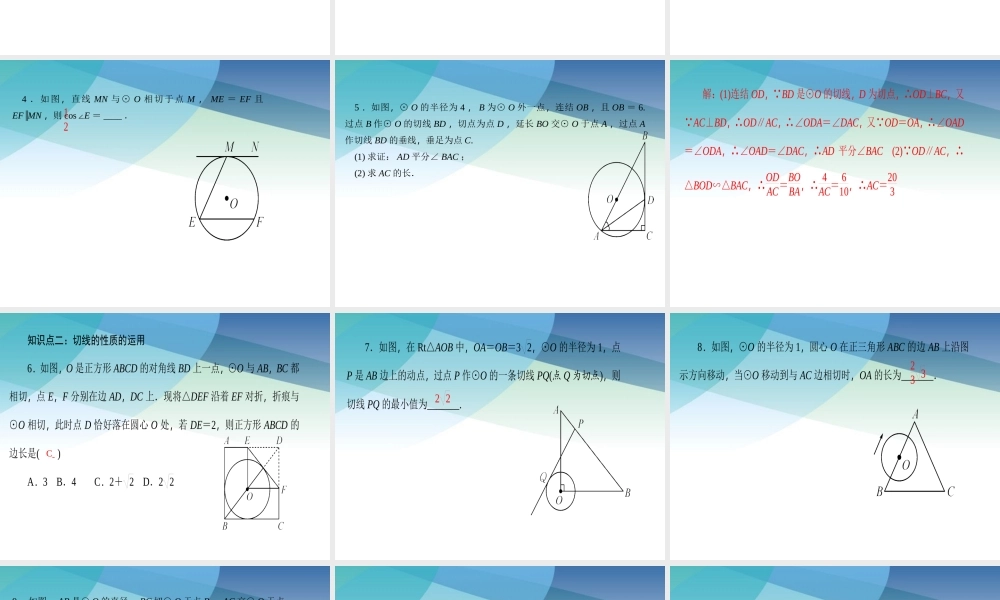
2.1直线与圆的位置关系第2章直线与圆的位置关系第3课时切线的性质圆的切线的性质:经过_________的半径____________圆的切线.切点垂直于知识点一:切线的性质1.如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是()A.30°B.45°C.60°D.40°A2.如图,AB是⊙O的直径,AC是⊙O的切线,连结OC交⊙O于点D,连结BD,∠C=40°,则∠ABD的度数是()A.30°B.25°C.20°D.15°B3.如图,⊙O的半径为3,P是CB延长线上一点,PO=5,PA切⊙O于A点,则PA=____.44.如图,直线MN与⊙O相切于点M,ME=EF且EF∥MN,则cos∠E=____.125.如图,⊙O的半径为4,B为⊙O外一点,连结OB,且OB=6.过点B作⊙O的切线BD,切点为点D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为点C.(1)求证:AD平分∠BAC;(2)求AC的长.解:(1)连结OD, BD是⊙O的切线,D为切点,∴OD⊥BC,又 AC⊥BD,∴OD∥AC,∴∠ODA=∠DAC,又 OD=OA,∴∠OAD=∠ODA,∴∠OAD=∠DAC,∴AD平分∠BAC(2) OD∥AC,∴△BOD∽△BAC,∴ODAC=BOBA,∴4AC=610,∴AC=203知识点二:切线的性质的运用6.如图,O是正方形ABCD的对角线BD上一点,⊙O与AB,BC都相切,点E,F分别在边AD,DC上.现将△DEF沿着EF对折,折痕与⊙O相切,此时点D恰好落在圆心O处,若DE=2,则正方形ABCD的边长是()A.3B.4C.2+2D.22C7.如图,在Rt△AOB中,OA=OB=32,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为_______.228.如图,⊙O的半径为1,圆心O在正三角形ABC的边AB上沿图示方向移动,当⊙O移动到与AC边相切时,OA的长为_______.2339.如图,AB是⊙O的直径,BC切⊙O于点B,AC交⊙O于点D.若∠A=30°,AD=2,求BC的长.解:4310.如图,在平面直角坐标系中,⊙P与x轴相切于原点O,平行于y轴的直线交⊙P于M,N两点.若点M的坐标是(2,-1),则点N的坐标是()A.(2,-4)B.(2,-4.5)C.(2,-5)D.(2,-5.5)A11.如图,直线AB与⊙O相切于点A,AC,CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为52,CD=4,则弦AC的长为______.2512.如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC,AB于点E,F.(1)若AC=6,AB=10,求⊙O的半径;(2)连结OE,ED,DF,EF,若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由.解:(1)连结OD,设⊙O的半...