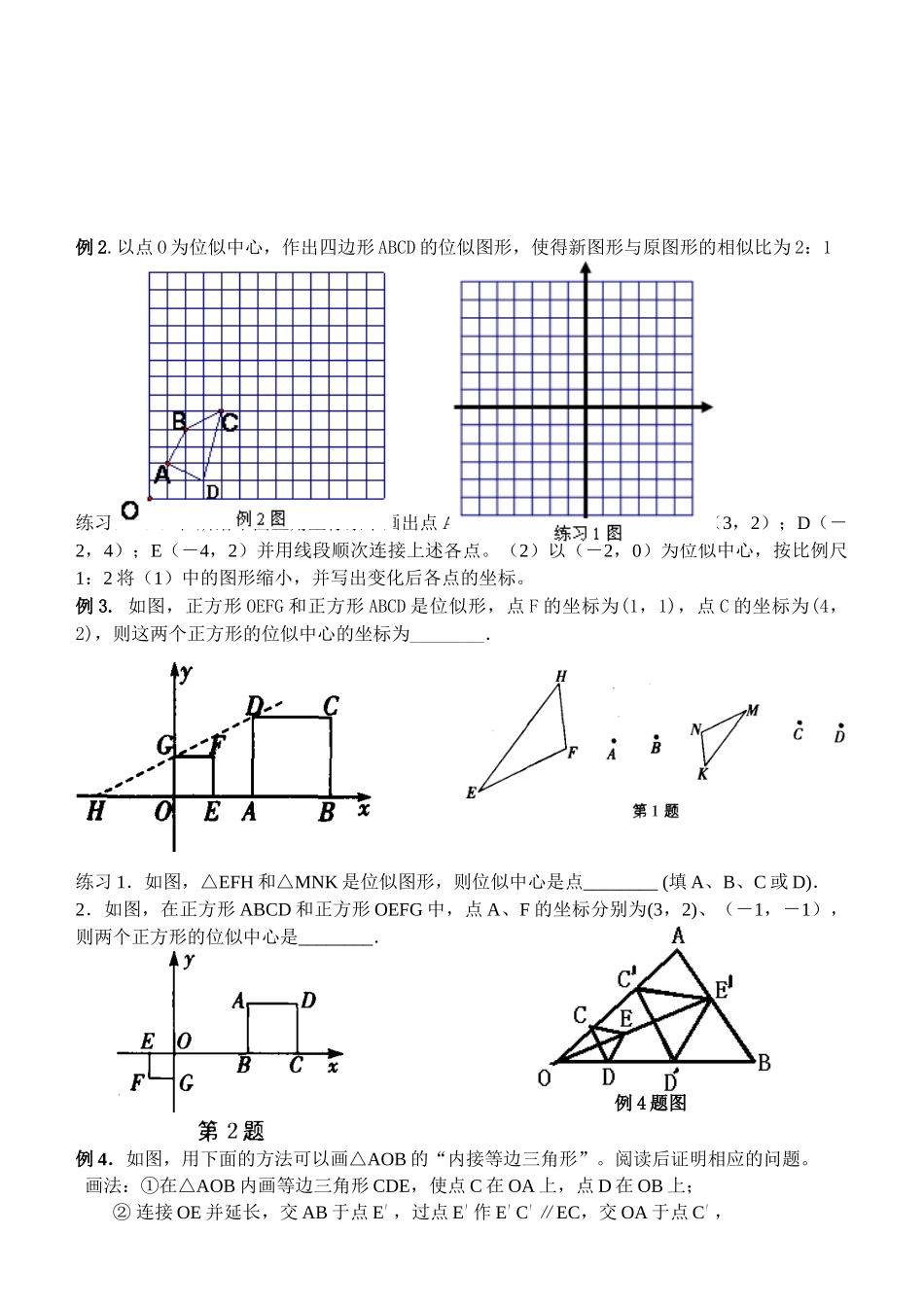
6.6图形的位似教学目标:1.了解位似多边形及其有关概念,了解位似与相似的联系和区别,掌握位似多边形的性质.2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.教学重点:位似多边形的有关概念、性质与作图.教学难点:利用位似将一个图形放大或缩小.课前参与:把幻灯片上的图形放大到屏幕上,形成的新图形和原图形就是典型的位似图形。1.位似形的相关概念如果两个图形相似,而且对应点的连线相交于一点,那么这两个图形叫做位似形,这个交点叫做位似中心.说明:位似形一定是相似形,但相似形不一定是位似形.2.位似形的意义及画法(1)意义:利用位似形可以将一个图形________或________.(2)画法:以△ABC为例,将△ABC扩大n倍(或缩小),得到△A'B'C'.①确定位似中心O,连接OA、OB、OC;②延长(或反向延长)OA、OB、OC;③在延长线(或反向延长线)OA上取OA'=n·OA,在延长线(或反向延长线)OB上取OB'=n·OB,在延长线(或反向延长线)OC上取OC'=n·OC;④顺次连接A'B'、B'C'、C'A',则△A'B'C'就是所画的图形.3.位似形的性质如图,若△A'B'C'与△ABC位似,相似比为k.(1) ,∠A'OC'=∠AOC,∴△________∽△________.∴________,同理,________.归纳:在位似形中,各对应点到位似中心的距离之比等于________。有时称位似图形的位似比就是相似比(注意:对应点重合除外).(2) ,∠A'OC'=∠AOC,∴△________∽△________.∴∠________=∠________.∴A'C'____AC.同理,B'C'____BC,A'B'_____AB.归纳:在位似形中,各对应边____________(注意:对应边所在的直线重合除外).课中参与:例1.分别以Q、D、C为位似中心画三角形,使它与△ABC(如图①)相似,且原三角形与所画三角形的相似比为2:1.例2.以点O为位似中心,作出四边形ABCD的位似图形,使得新图形与原图形的相似比为2:1练习:(1)在所给平面直角坐标系中画出点A(-4,0);B(2,-3);C(3,2);D(-2,4);E(-4,2)并用线段顺次连接上述各点。(2)以(-2,0)为位似中心,按比例尺1:2将(1)中的图形缩小,并写出变化后各点的坐标。例3.如图,正方形OEFG和正方形ABCD是位似形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形的位似中心的坐标为________.练习1.如图,△EFH和△MNK是位似图形,则位似中心是点________(填A、B、C或D).2.如图,在正方形ABCD和正方形OEFG中,点A、F的坐标分别为(3,2)、(-1,-1),...