九年级下册数学苏科7.2 正弦、余弦.docVIP免费

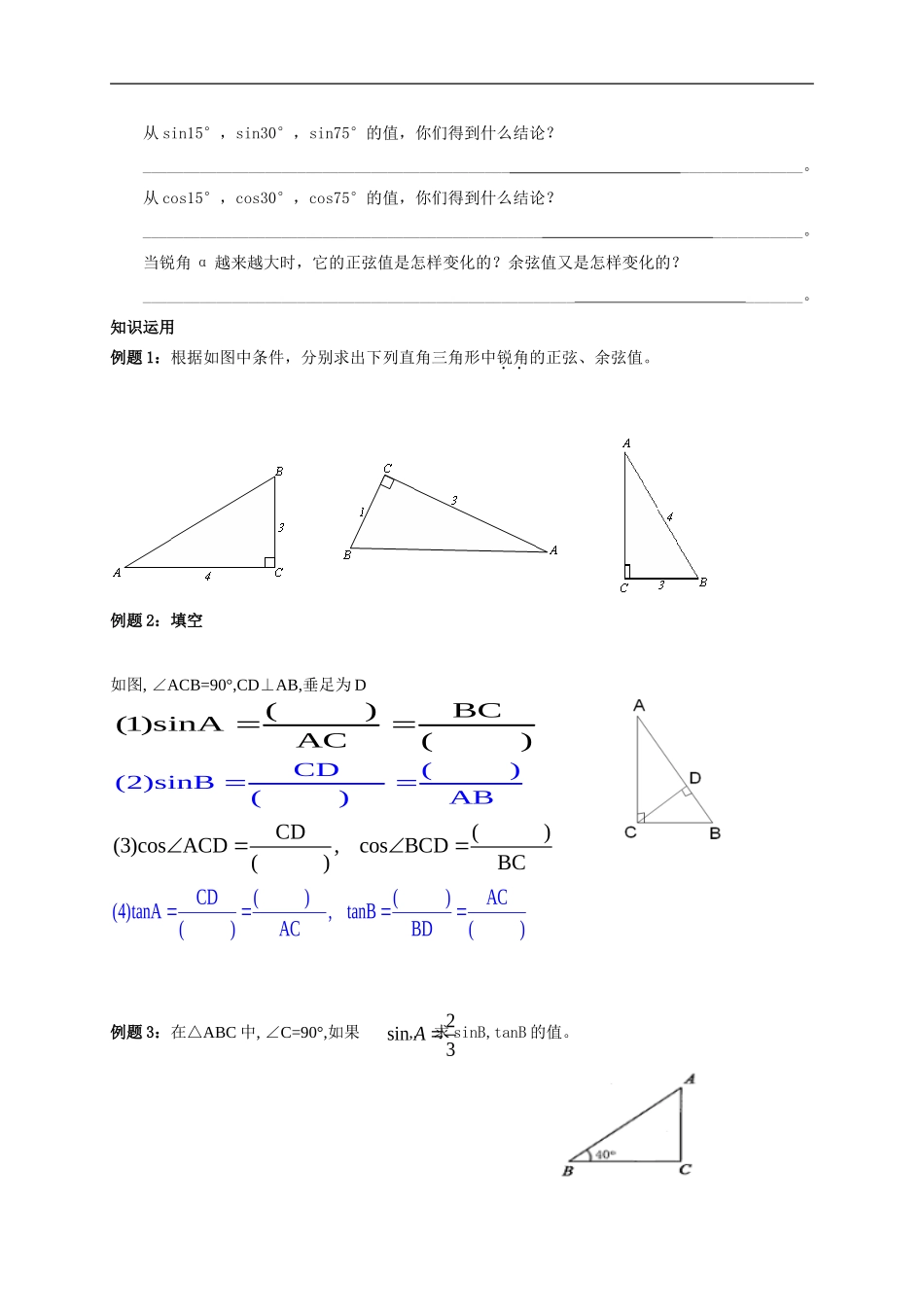
7.2正弦、余弦课前准备问题：如图，小明沿着某斜坡向上行走了13m后，他的相对位置升高了5m，如果他沿着该斜坡行走了20m，那么他的相对位置升高了多少？行走了am呢？可求出∠A的对边与斜边之比为。以上情况下∠A的邻边与斜边的比值又如何？探究新知1．思考：从上面的两个问题可以看出：当直角三角形的一个锐角的大小已确定时，它的对边与斜边的比值__________；它的邻边与斜边的比值___________。（根据是______________________________________。）2．正弦的定义如图，在Rt△ABC中，∠C＝90°，我们把锐角∠A的对边a与斜边c的比叫做∠A的______，记作____，即：sinA＝________=________.3．余弦的定义如图，在Rt△ABC中，∠C＝90°,我们把锐角∠A的邻边b与斜边c的比叫做∠A的______，记作_____，即：cosA=______=_____。（你能写出∠B的正弦、余弦的表达式吗？）试试看.___________________________________________________.4．锐角A的正弦、余弦和正切都是∠A的__________。5．思考与探索怎样计算任意一个锐角的正弦值和余弦值呢？（1）书P42图7—8（2）你能根据图形求出sin30°、cos30°吗？sin75°、cos75°呢？sin30°＝_____，cos30°＝_____.sin75°＝_____，cos75°＝_____.（3）利用计算器我们可以更快、更精确地求得各个锐角的正弦值和余弦值。（4）观察与思考：20m13m从sin15°，sin30°，sin75°的值，你们得到什么结论？____________________________________________________________。从cos15°，cos30°，cos75°的值，你们得到什么结论？____________________________________________________________。当锐角α越来越大时，它的正弦值是怎样变化的？余弦值又是怎样变化的？____________________________________________________________。知识运用例题1：根据如图中条件，分别求出下列直角三角形中锐角的正弦、余弦值。例题2：填空如图,∠ACB=90°,CD⊥AB,垂足为D例题3：在△ABC中,∠C=90°,如果,.求sinB,tanB的值。()BC(1)sinAAC()CD()(2)sinB()ABCD()(3)cosACD,cosBCD()BCCD()()AC(4)tanA,tanB()ACBD()2sin3A当堂反馈1．如图，在Rt△ABC中，∠C＝90°，AC＝12，BC＝5，则sinA＝_____，cosA＝_____，sinB＝_____，cosB＝_____。2.在Rt△ABC中，∠C＝90°，AC＝1，AB＝2，则sinA＝_____，cosB=_______,cosA=________,sinB=_______.3．如图,已知直角三角形ABC中，斜边AB的长为m，∠B=40°，则直角边...