23.2 第2课时仰角与俯角问题.pptVIP免费

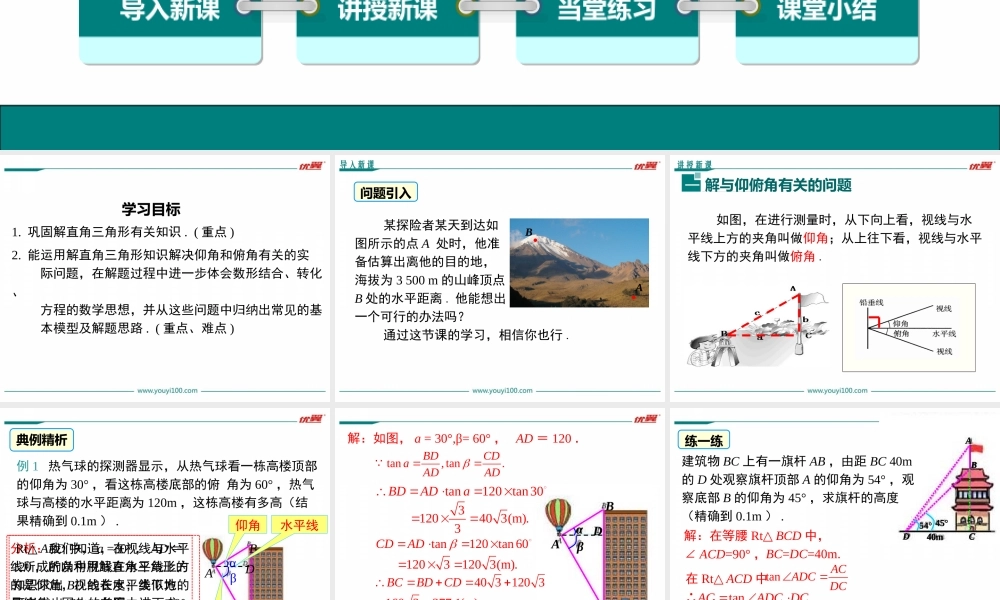
23.2解直角三角形及其应用优翼课件导入新课讲授新课当堂练习课堂小结第2课时仰角与俯角问题九年级数学上（HK）教学课件学习目标1.巩固解直角三角形有关知识.(重点)2.能运用解直角三角形知识解决仰角和俯角有关的实际问题，在解题过程中进一步体会数形结合、转化、方程的数学思想，并从这些问题中归纳出常见的基本模型及解题思路.(重点、难点)导入新课某探险者某天到达如图所示的点A处时，他准备估算出离他的目的地，海拔为3500m的山峰顶点B处的水平距离.他能想出一个可行的办法吗？通过这节课的学习，相信你也行.．AB．．问题引入讲授新课解与仰俯角有关的问题一如图，在进行测量时，从下向上看，视线与水平线上方的夹角叫做仰角；从上往下看，视线与水平线下方的夹角叫做俯角.例1热气球的探测器显示，从热气球看一栋高楼顶部的仰角为30°，看这栋高楼底部的俯角为60°，热气球与高楼的水平距离为120m，这栋高楼有多高（结果精确到0.1m）.ABCDαβ仰角水平线俯角分析：我们知道，在视线与水平线所成的角中视线在水平线上方的是仰角，视线在水平线下方的是俯角，因此，在图中，a=30°，β=60°.典例精析Rt△ABD中，a=30°，AD＝120，所以利用解直角三角形的知识求出BD的长度；类似地可以求出CD的长度，进而求出BC的长度，即求出这栋楼的高度.解：如图，a=30°,β=60°，AD＝120．tan,tan.BDCDaADAD3120403(m).312031203(m).答：这栋楼高约为277.1m.ABCDαβtan120tan30BDADatan120tan60CDAD4031203BCBDCD1603277.1(m).建筑物BC上有一旗杆AB，由距BC40m的D处观察旗杆顶部A的仰角为54°，观察底部B的仰角为45°，求旗杆的高度（精确到0.1m）.ABCD40m54°45°ABCD40m54°45°解：在等腰Rt△BCD中，∠ACD=90°，BC=DC=40m.在Rt△ACD中，tanACADCDCtanACADCDC∴tan54401.384055.2m，∴AB=AC－BC=55.2－40=15.2(m).练一练例3一学生要测量校园内一棵水杉树的高度.他站在距离水杉树8m的E处,测得树顶的仰角∠ACD=52°，已知测角器的架高CE=1.6m.问树高AB为多少米？（精确到0.1m）解：在Rt△ACD中，∠ACD=52°，CD=EB=8m.由tan∠ACD=，得AD=CD·tan∠ACD=8×tan52°=8×1.2799≈10.2（m）.由DB=CE=1.6m，得AB=AD+DB=10.2+1.6=11.8（m）.答：树高AB为11.8m.ADCD例4解决本章引言所提问题.如图，某校九年级学生要测量当地电视塔的高度AB，因为不能直接到达塔底B处，他们采...