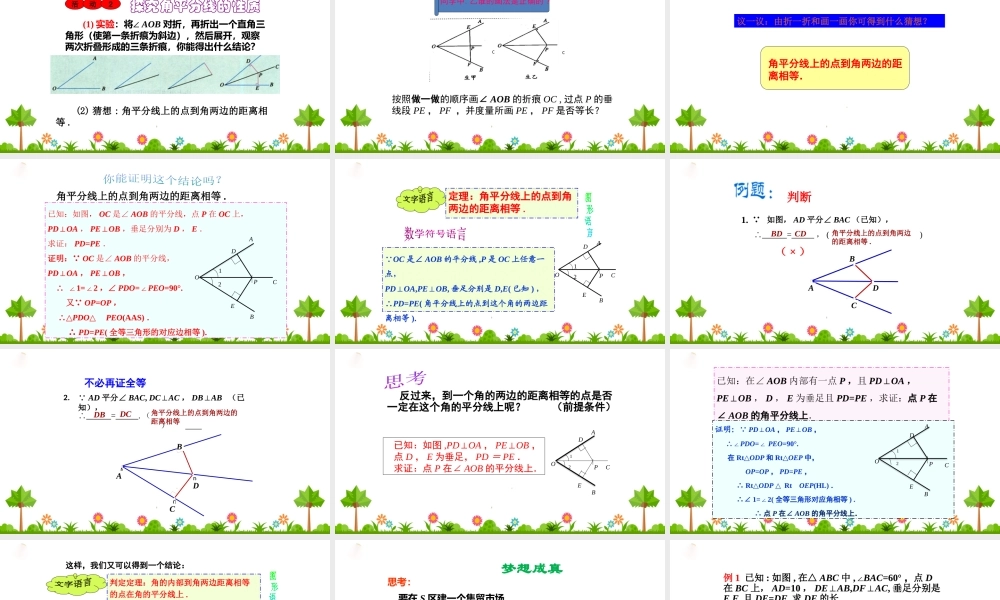
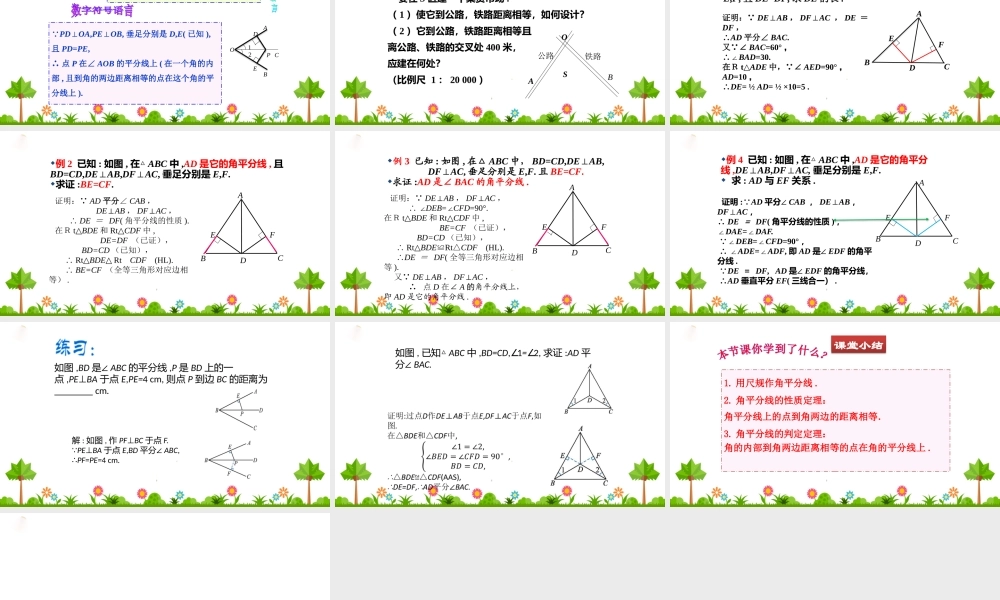
2.4线段、角的轴对称性(2)探究角平分线的性质(1)实验:将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?活动2(2)猜想:角平分线上的点到角两边的距离相等.同学甲、乙谁的画法是正确的?按照做一做的顺序画∠AOB的折痕OC,过点P的垂线段PE,PF,并度量所画PE,PF是否等长?CC角平分线上的点到角两边的距离相等.议一议:由折一折和画一画你可得到什么猜想?已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:PD=PE.证明: OC是∠AOB的平分线,PD⊥OA,PE⊥OB,∴∠1=2∠,∠PDO=∠PEO=90°.又 OP=OP,∴△PDO△PEO(AAS).∴PD=PE(全等三角形的对应边相等).AOCB12PDE角平分线上的点到角两边的距离相等.定理:角平分线上的点到角两边的距离相等. OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E(已知),∴PD=PE(角平分线上的点到这个角的两边距离相等).AOCB12PDE 如图,AD平分∠BAC(已知),∴=,()角平分线上的点到角两边的距离相等.ADCBBDCD(×)判断1.ABCD AD平分∠BAC,DC⊥AC,DB⊥AB(已知),∴=.()DBDC角平分线上的点到角两边的距离相等ADCB不必再证全等2.ABCD反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢?(前提条件)已知:如图,PD⊥OA,PE⊥OB,点D,E为垂足,PD=PE.求证:点P在∠AOB的平分线上.AOCB12PDE已知:在∠AOB内部有一点P,且PD⊥OA,PE⊥OB,D,E为垂足且PD=PE,求证:点P在∠AOB的角平分线上.证明: PD⊥OA,PE⊥OB,∴∠PDO=∠PEO=90°.在Rt△ODP和Rt△OEP中,OP=OP,PD=PE,∴Rt△ODPRt△△OEP(HL).∴∠1=2(∠全等三角形对应角相等).∴点P在∠AOB的角平分线上.AOCB12PDE判定定理:角的内部到角两边距离相等的点在角的平分线上. PD⊥OA,PE⊥OB,垂足分别是D,E(已知),且PD=PE,∴点P在∠AOB的平分线上(在一个角的内部,且到角的两边距离相等的点在这个角的平分线上).AOCB12PDE这样,我们又可以得到一个结论:梦想成真AB思考:要在S区建一个集贸市场.(1)使它到公路,铁路距离相等,如何设计?(2)它到公路,铁路距离相等且离公路、铁路的交叉处400米,应建在何处?(比例尺1:20000)SO公路铁路例1已知:如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别是E,F,且DE=DF,求DE的长.ABCDEF证明: DE⊥AB,DF⊥AC,DE=DF,∴AD平分∠BAC.又 ∠...