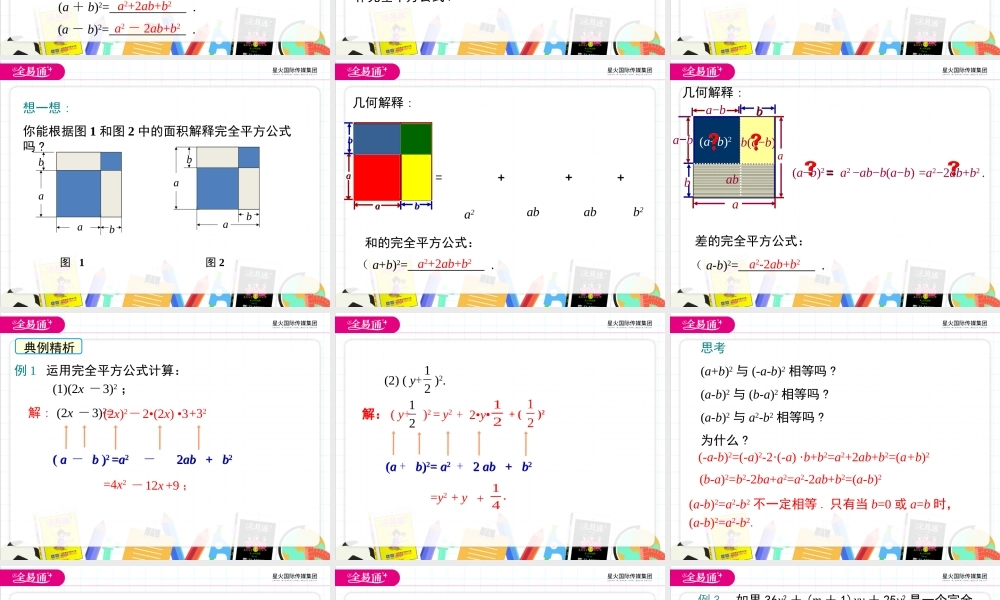
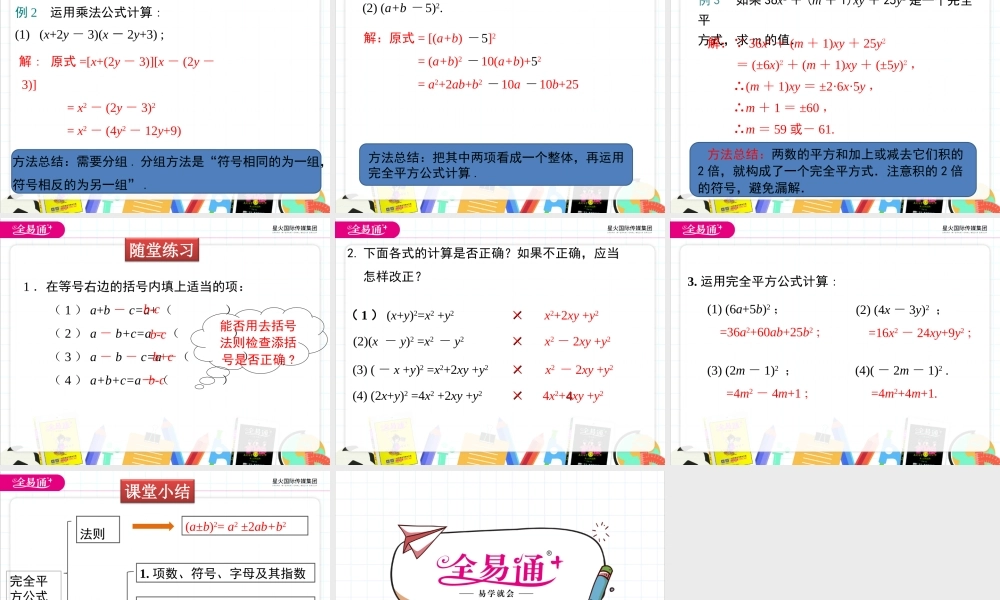
第一章整式的乘除6完全平方公式(第1课时)1.理解并掌握完全平方公式的推导过程、结构特点;(重点)2.会运用公式进行简单的运算;(难点)学习目标平方差公式:(a+b)(a-b)=a2-b22.公式的结构特点:左边是两个二项式的乘积,即两数和与这两数差的积;右边是两数的平方差.1.由下面的两个图形你能得到哪个公式?复习巩固导入新课情境引入一块边长为a米的正方形实验田,因需要将其边长增加b米.形成四块实验田,以种植不同的新品种(如图).用不同的形式表示实验田的总面积,并进行比较.你发现了什么?aaaabbbb直接求:总面积=(a+b)(a+b)间接求:总面积=a2+ab+ab+b2(a+b)2=a2+2ab+b2完全平方公式计算下列多项式的积,你能发现什么规律?(1)(p+1)2=(p+1)(p+1)=.p2+2p+1(2)(m+2)2=(m+2)(m+2)=.m2+4m+4(3)(p-1)2=(p-1)(p-1)=.p2-2p+1(4)(m-2)2=(m-2)(m-2)=.m2-4m+4根据上面的规律,你能直接下面式子的写出答案吗?(a+b)2=.a2+2ab+b2(a-b)2=.a2-2ab+b2讲授新课知识要点完全平方公式(a+b)2=.a2+2ab+b2(a-b)2=.a2-2ab+b2两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫作完全平方公式.简记为:“首平方,尾平方,积的2倍放中间”公式特征:1.积为二次三项式;2.积中的两项为两数的平方;3.另一项是两数积的2倍,且与乘式中间的符号相同.4.公式中的字母a,b可以表示数,单项式和多项式.你能根据图1和图2中的面积解释完全平方公式吗?baabbaba图1图2想一想:几何解释:aaaabbbb=+++a2ababb2(a+b)2=.a2+2ab+b2和的完全平方公式:a2−ab−b(a−b)=a2−2ab+b2.==(a−b)2a−ba−baaabb(a−b)bbb(a−b)2几何解释:(a-b)2=.a2-2ab+b2差的完全平方公式:典例精析例1运用完全平方公式计算:解:(2x-3)2==4x2(1)(2x-3)2;((aa-bb))22==aa22-22abab++bb22(2x)2-2•(2x)•3+32-12x+9;((aa+bb))22==aa22+22abab++bb22y2(2)(y+)2.21=y2+y+1.4+()212+2•y•12解:(y+)2=21思考(a+b)2与(-a-b)2相等吗?(a-b)2与(b-a)2相等吗?(a-b)2与a2-b2相等吗?为什么?(-a-b)2=(-a)2-2·(-a)·b+b2=a2+2ab+b2=(a+b)2(b-a)2=b2-2ba+a2=a2-2ab+b2=(a-b)2(a-b)2=a2-b2不一定相等.只有当b=0或a=b时,(a-b)2=a2-b2.例2运用乘法公式计算:(1)(x+2y-3)(x-2y+3);解:原式=[x+(2y-3)][x-(2y-3)]=x2-(2y-3)2=x2-(4y2-12y+9)=x2-4y2+12y-9.方法总结:需要分组.分组方法是“符号相同的为一组,符号相反的为另一组”.(2)(a+b-...