1.4 第1课时 单项式与单项式相乘.pptVIP免费

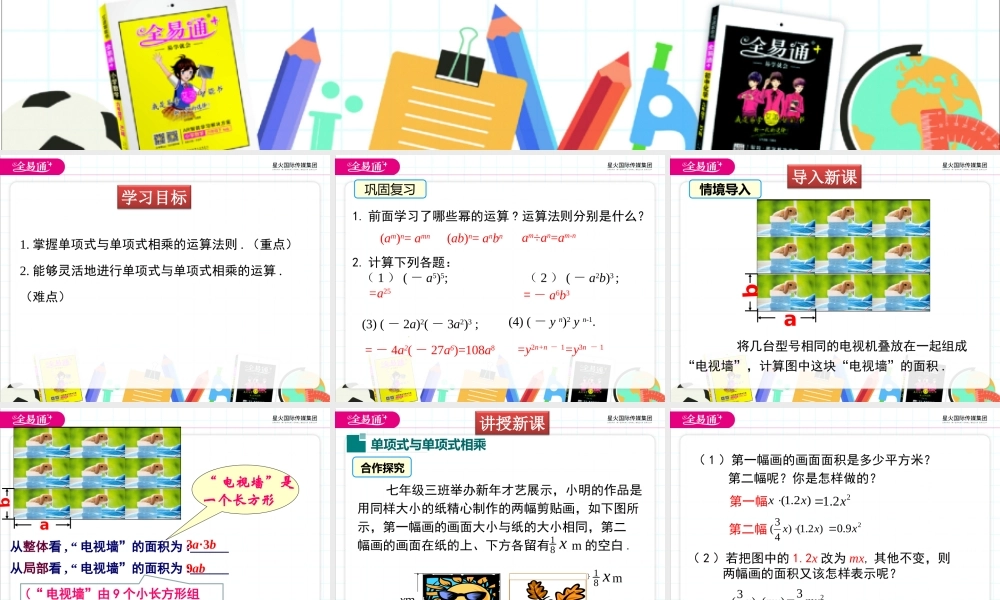
第一章整式的乘除1.4整式的乘法（第1课时）1.掌握单项式与单项式相乘的运算法则.（重点）2.能够灵活地进行单项式与单项式相乘的运算.（难点）学习目标1.前面学习了哪些幂的运算?运算法则分别是什么？2.计算下列各题：（1）(－a5)5;（2）(－a2b)3;=a25(3)(－2a)2(－3a2)3;=－4a2(－27a6)=108a8(4)(－yn)2yn-1.am÷an=am-n(am)n=amn(ab)n=anbn巩固复习=－a6b3=y2n+n－1=y3n－1情境导入ab将几台型号相同的电视机叠放在一起组成“电视墙”，计算图中这块“电视墙”的面积.导入新课ab从整体看,“电视墙”的面积为:______从局部看,“电视墙”的面积为:______3a·3b9ab“电视墙”是一个长方形(“电视墙”由9个小长方形组成).你发现了什么?3a·3b=9ab七年级三班举办新年才艺展示，小明的作品是用同样大小的纸精心制作的两幅剪贴画，如下图所示，第一幅画的画面大小与纸的大小相同，第二幅画的画面在纸的上、下方各留有m的空白.1.2xmx81xmx81x81mm单项式与单项式相乘合作探究讲授新课（1）第一幅画的画面面积是多少平方米？第二幅呢？你是怎样做的？（2）若把图中的1.2x改为mx,其他不变，则两幅画的面积又该怎样表示呢？)2.1(xx)2.1()43(xx22.1x29.0x第一幅第二幅)()43(mxx243mx1.2x²y·3xy²和4a2x5·(-3a3bx)又等于什么？你是怎样计算的？2.如何进行单项式乘单项式的运算？3.在你探索单项式乘法运算法则的过程中，运用了哪些运算律和运算法则？交流讨论(1)2x2y·3xy2=(2×3)(x2·x)(y·y2)=6x3y3；(利用乘法交换律、结合律将系数与系数，相同字母分别结合，有理数的乘法、同底数幂的乘法)(2)4a2x5·(-3a3bx)=[4×(－3)](a2·a3)·b·(x5·x)=－12a5bx6．(字母b只在一个单项式中出现，这个字母及其指数不变)单项式与单项式相乘，把它们的系数、同底数幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式.知识要点单项式与单项式的乘法法则（1）系数相乘；（2）相同字母的幂相乘；（3）其余字母连同它的指数不变，作为积的因式.注意典例精析例1计算：(1)2xy2•xy;(2)(－2a2b3•(－3a)；(3)7xy2z•(2xyz)2.解:(1)原式=(2×)•(x•x)•(y2•y)=(2)原式=[(－2)×(－3)]•(a2a)•b3=6a3b3;3131;3232yx(3)原式=7xy2z•4x2y2z2=(7×4)•(xx2)•(y2y2)•(zz2)=28x3y4z3.单项式与单项式相乘有理数的乘法与同底数幂的乘法乘法交换律和结合律转化方法总结计算：(1)(－3x)2·4x2；(2)(－2a)3(－3a)2；解：原式=9x2·4x2=(9×4)(x...