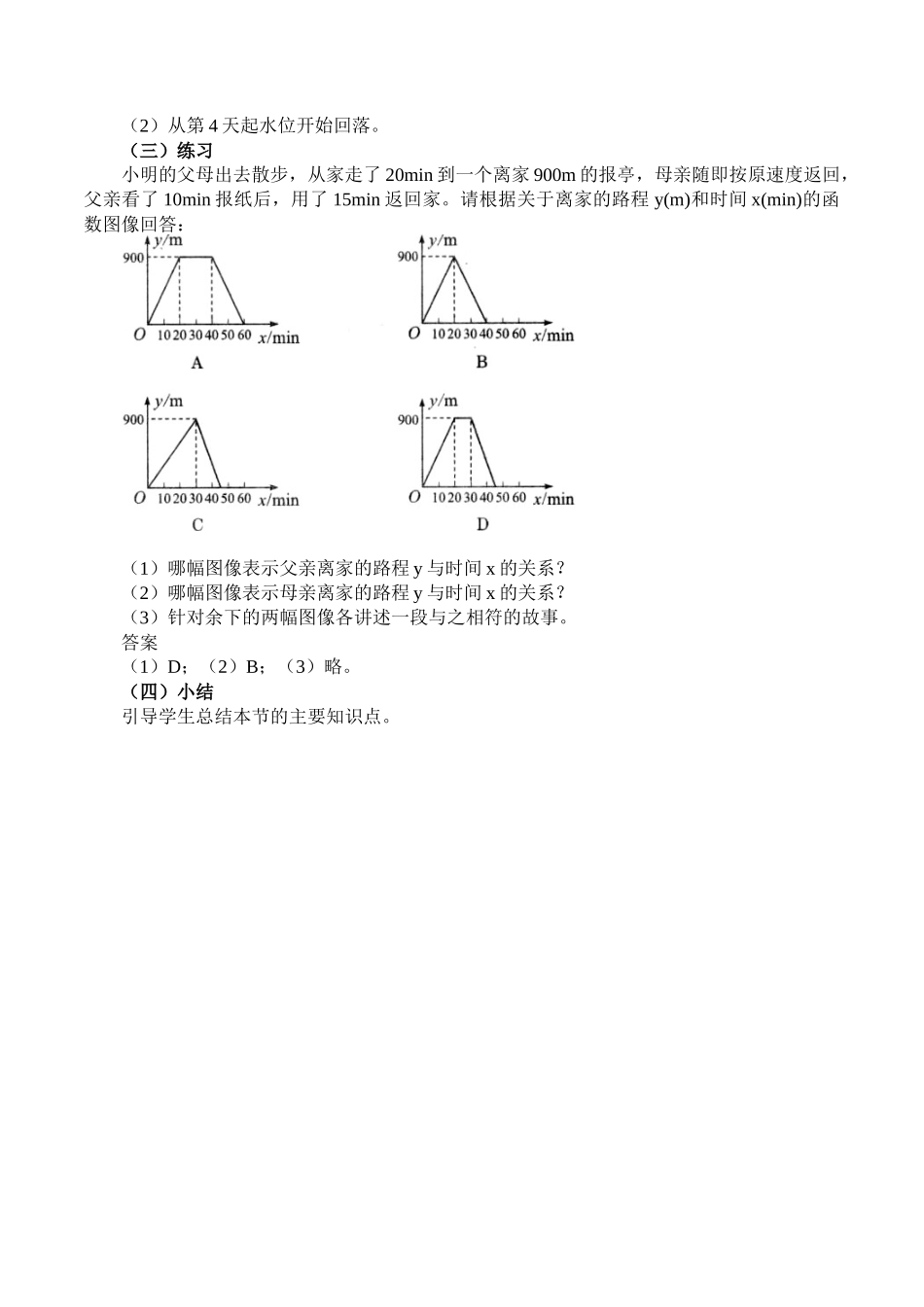
函数的表示【教学目标】(一)知识与技能1.通过实例了解函数的三种表示方法;2.从具体问题中了解函数各种表示方法的特点。能选择恰当的方法表示实际问题中函数的关系。(二)过程与方法经历动手操作、探究和合作交流的过程,进一步体会各种表示方法的特点。(三)情感态度价值观初步体会数形结合的思想方法。【教学重点】函数关系的三种表示方法。【教学难点】对于具体问题能灵活运用这三种表示方法中的某种进行分析。【教学方法】合作探究、小组讨论。【教学过程】用适当的方法表示函数,能够帮助我们更好地认识函数,并运用函数解决问题。我们已经看到,用表达式、图形、表格等都可以表示两个变量之间的函数关系。现在,我们对这些表示方法作进一步的研究。人们发现,声音在空气中传播的速度(简称音速)随气温的变化而变化。某研究者通过实验得到了这样一些关于气温x与音速y对应的数据:x/℃-10-505101520y/(m/s)325.36328.36331.36334.36337.36340.36343.36实际上,这就是用表格表示的关于音速y与气温x之间的函数关系。(一)一起探究1.你还能用其他方法表示音速y与气温x之间的函数关系吗?2.这些表示方法有什么特点?在前面学习函数的基础上,探究把表格表示的函数关系用表达式和图形来表示。从表格中可以看出,气温x每升高(或降低)5()℃,音速y就增加(或减少)3(m/s)。也就是说,气温x每升高(或降低)1()℃,音速y就增加(或减少)35(m/s)。而当x=0时,)y=331.36(m/s)。这样,音速y(m/s)和气温x()℃之间的函数关系就可以表示为3yx331.365。这个表达式更加全面、准确地反映了音速y(m/s)和气温x()℃之间的对应关系。利用它,可以方便地得到与x()℃值对应的y(m/s)的值。如,当气温x为-4()℃时,音速y为3(4)331.36=328.965(m/s),当气温x为28()℃时,音速y为328331.36=348.165(m/s)……音速y(m/s)与气温x()℃之间的函数关系,还可以借助于图形表示出来,具体可以这样做:1.画出直角坐标系,用横轴上的点表示气温x()℃,用纵轴上的点表示音速y(m/s),如图21—4所示。2.借助于表格(或表达式),找出x和y的若干对对应值,如(-5,328.36),(0,331.36),(5,334.36),(10,337.36),(15,340.36),…。分别以每对值为横、纵坐标,确定出坐标系中相应的点。3.用平滑的线将这些点连结,就得到音速y(m/s)和气温x()℃之间用图形表示的函数关系。把一个函数的自变量x的值与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系内描...