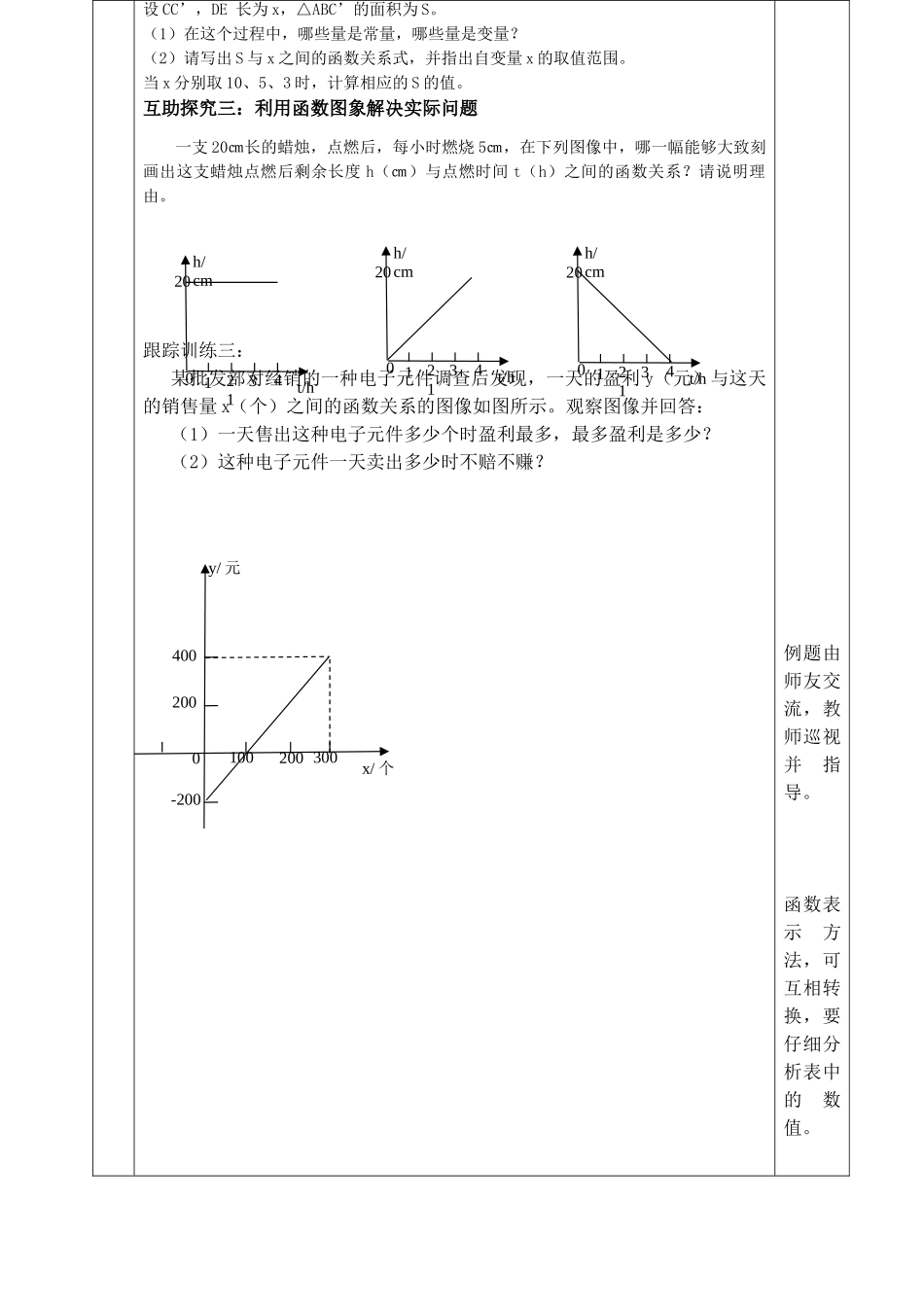
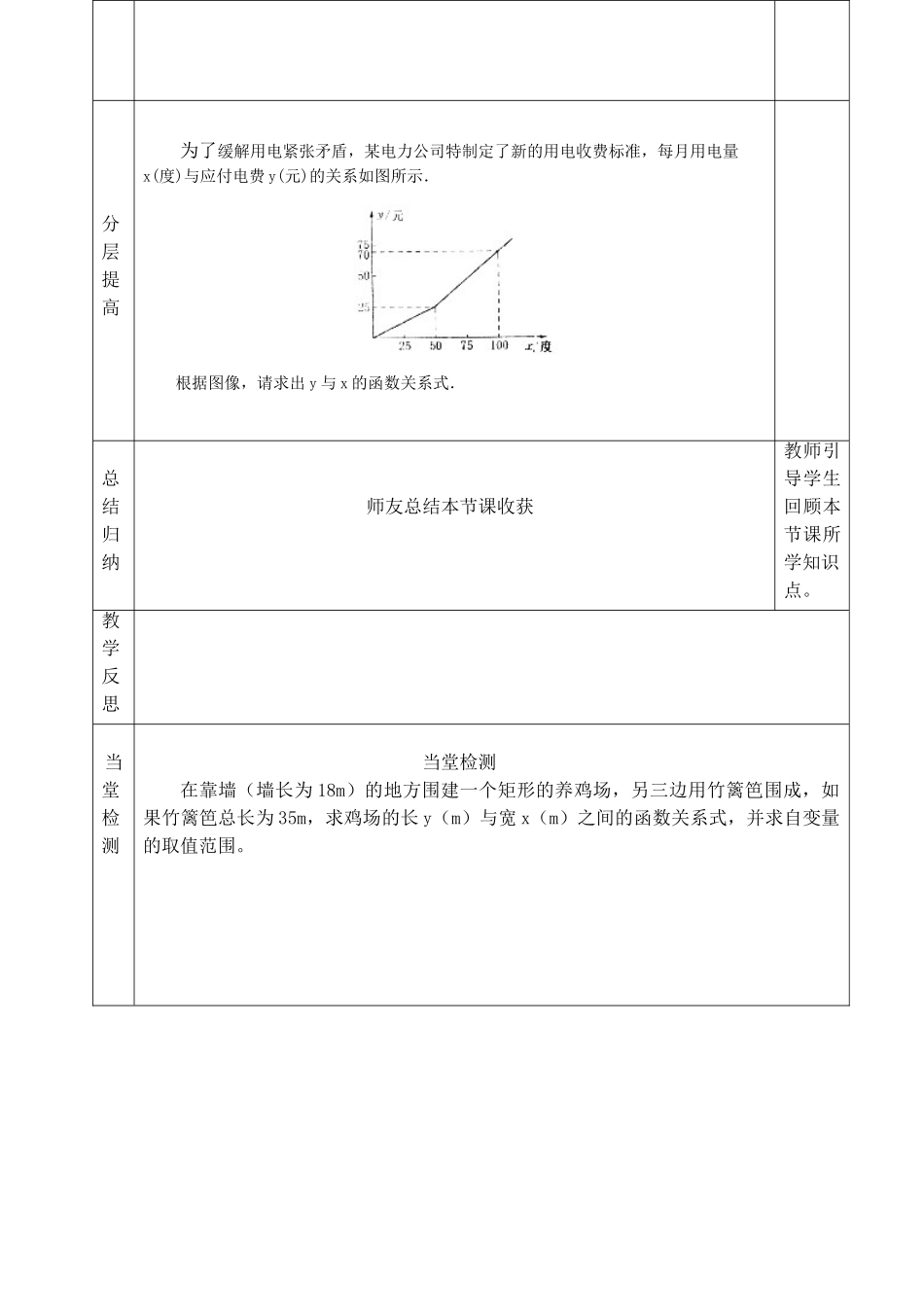
课题20.4函数的初步应用主备人审核课型新授课课时1课时时间学习目标1.能从函数关系中获取相应信息,运用函数解决简单的实际问题。2体会函数模型的作用,增强数学应用意识。重点难点重点:数形结合思想的应用。难点:从函数关系中获取相应信息,运用函数解决简单的实际问题。学习过程教学环节互助学习教师点拨互助探究互助探究一函数在数量型关系的应用已知摄氏温度值和华氏温度值有下表所示的对应关系:摄氏温度/℃01020304050华氏温度/°F32506886104122(1)当摄氏温度为30℃时,华氏温度为多少?(2)当摄氏温度为36℃时,由数值表能直接求出华氏温度吗?试写出这两种温度之间关系的函数表达式,并求摄氏温度为36℃时的华氏温度。(3)当华氏温度为140°F时,摄氏温度时多少?跟踪训练一:1、一辆汽车的油箱内有油48升,从某地出发,每行驶1千米,耗油0.6升,如果设剩油量为y升,行驶路程为x千米。(1)写出x与y的关系式。(2)用表格表示汽车从出发地行驶10千米,20千米,30千米,40千米,50千米时的剩油量。(3)根据表格中的数据说明剩油量时怎样随着行驶路程的变化而变化的。互助探究二:函数在图形问题中的应用例:一圆锥的高是20㎝,当底面半径r(㎝)由1㎝变化到10㎝时,圆锥的体积V(㎝3)也在变化。(1)请写出V与r之间的函数关系式,并指出自变量的取值范围。(2)完成下表:r(㎝)135910V(㎝3)60π跟踪训练二:在△ABC中,BC=16,高AD=10.动点C’由点C沿CB向点B移动(不与点B重合)。教师引导学生师友互助探究知识点。构建函数模型,解决实际问题。设CC’,DE长为x,△ABC’的面积为S。(1)在这个过程中,哪些量是常量,哪些量是变量?(2)请写出S与x之间的函数关系式,并指出自变量x的取值范围。当x分别取10、5、3时,计算相应的S的值。互助探究三:利用函数图象解决实际问题一支20㎝长的蜡烛,点燃后,每小时燃烧5㎝,在下列图像中,哪一幅能够大致刻画出这支蜡烛点燃后剩余长度h(㎝)与点燃时间t(h)之间的函数关系?请说明理由。跟踪训练三:某批发部对经销的一种电子元件调查后发现,一天的盈利y(元)与这天的销售量x(个)之间的函数关系的图像如图所示。观察图像并回答:(1)一天售出这种电子元件多少个时盈利最多,最多盈利是多少?(2)这种电子元件一天卖出多少时不赔不赚?例题由师友交流,教师巡视并指导。函数表示方法,可互相转换,要仔细分析表中的数值。20h/cmt/h01213420h/cmt/h01213420h/cmt/h0121342002...