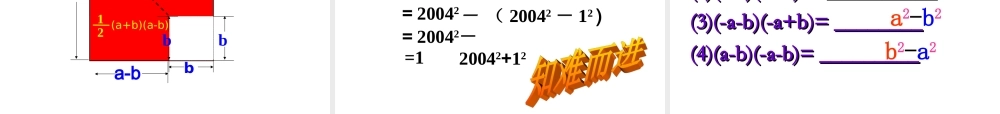沪教版(五四学制)七上：9.11 平方差公式（1） 课件（31张ppt）.pptVIP免费

复习：多项式与多项式相乘的法则(a+b)(m+n)=am+an+bm+bn多项式与多项式相乘，先用多项式与多项式相乘，先用一个多项式的一个多项式的每一项每一项乘以另一个多乘以另一个多项式的项式的每一项，每一项，再把所得的再把所得的积相加。积相加。计算下列多项式的积：①（x＋2)(x－2）②（1＋3a)(1－3a）③（m＋5n)(m－5n）=x2－4=1－9a2=m2－25n=9y2－z2=x2－22=12－(3a)2=m2－(5n2=(3y)2－z2②（1＋3a)(1－3a）=③（m＋5n)(m－5n)=④（3y＋z)(3y－z)=①（x＋2)(x－2）=x2－2212－(3a)2m2－(5n)2(3y)2－z2猜想(a+b)(a-b)=a2-b2(a+b)(a-b)=a2-b21、代数法验证bb22ababab22、、图形验证：图形验证：a-ba-bba(a+b)(a-b)=a2-b2(a+b)(a-b)=a2-b2这两个数的差这两数的平方差两个数的和用语言叙述平方差公式两个数的和与这两个数的差的乘积，等于这两个数的平方差。说明：公式中的a,b可以是任意的数或代数式。(a+b)(a-b)=a2-b2结构特征:相同项相反项(相同项)2-(相反项)2两个数的和与这两个数的差的积，等于这两个数的平方差。两个二项式相乘(1+x)(1-x)(-3+a)(-3-a)(0.3x-1)(1+0.3x)(1+a)(-1+a)11、找一找、填一填、找一找、填一填相同项a相反项b1x-3aa10.3x1(a+b)(a-b)(a+b)(a-b)2、下列各式能否用平方差公式进行计算(2)(x+3)(y-3)(3)(m-n)(n-m)(1)(-m+n)(-m-n)(4)(m-3)(-3-m)((aa++bb)()(aa−−bb))==aa22−−bb22(a+b)(a–b)=a2-b2找出哪个是找出哪个是相同项相同项,,哪个是哪个是相反项相反项例1、计算：(1)(2)(-x+3y)(-x-3y).(3)(y＋2x)(2x－y))3121)(3121(yxyx2、(8＋ab)(ab－8)1、(5＋x)(－x+5)33、计算、计算)221)(221(、4yxyx((aa++bb)()(aa−−bb))==aa22−−bb22))((32222yxyx、例2.利用平方差公式计算（1）9.8×10.2989991100)2(•练习4、计算•（1）50.2×49.8•（2）769×7110有一个狡猾的地主,把一边长为a米的正方形土地租给王大爷。有一天他对王大爷说:“我把这块地的一边增加5米,另一边减少5米,继续租给你,你也没吃亏,如何?王大爷一听觉得是没吃亏,就答应了。回到家,他就把这件事告诉了邻居,邻居一听,说:“王大爷您吃亏了!”王大爷非常不解,同学们,你能告诉王大爷这是为什么吗?5米5米a(a-5)(a+5)原来原来现在现在a2(a+5)(a-5)能否运用平方差公式计算：()()?abcabcabab12(a+b)(a-b)12(a+b)(a-b)ba-b))((212babababa1.计算20042－2003×2005;解：20042－2003×2005=20042－(200...