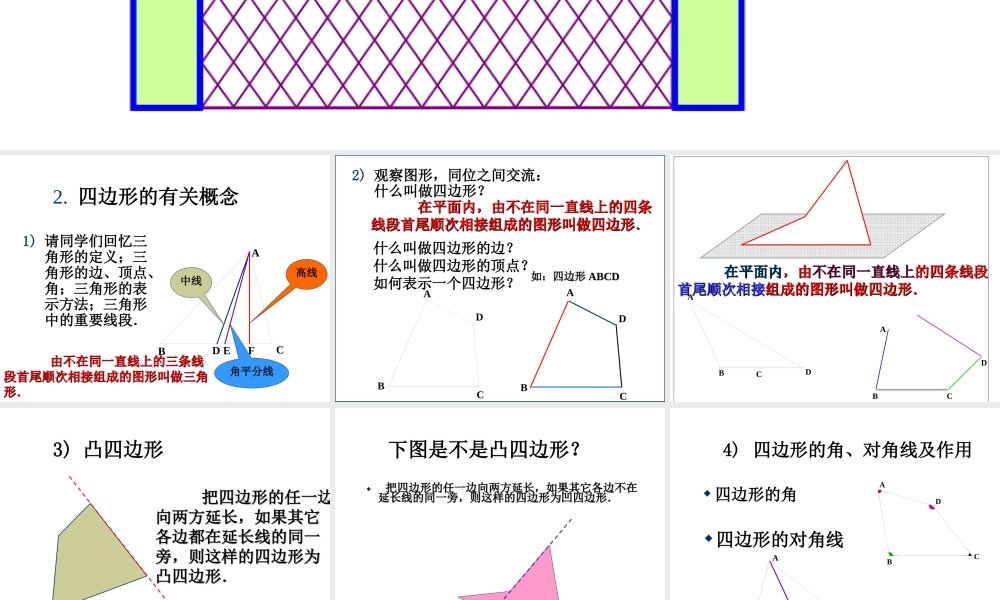
1.1.引入课引入课题题四边形四边形2.四边形的有关概念1)请同学们回忆三角形的定义;三角形的边、顶点、角;三角形的表示方法;三角形中的重要线段.ABCD中线F高线E角平分线由不在同一直线上的三条线由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角段首尾顺次相接组成的图形叫做三角形.形.2)观察图形,同位之间交流:什么叫做四边形?ABCD在平面内,由不在同一直线上的四条在平面内,由不在同一直线上的四条线段首尾顺次相接组成的图形叫做四边形.线段首尾顺次相接组成的图形叫做四边形.ABCD什么叫做四边形的边?什么叫做四边形的顶点?如何表示一个四边形?如:四边形如:四边形ABCDABCD在平面内在平面内,由,由不在同一直线上不在同一直线上的四条线段的四条线段首尾顺次相接首尾顺次相接组成的图形叫做四边形.组成的图形叫做四边形.ABDCABCD3)凸四边形把四边形的任一边把四边形的任一边向两方延长,如果其它向两方延长,如果其它各边都在延长线的同一各边都在延长线的同一旁,则这样的四边形为旁,则这样的四边形为凸四边形.凸四边形.下图是不是凸四边形?把四边形的任一边向两方延长,如果其它各边不在把四边形的任一边向两方延长,如果其它各边不在延长线的同一旁,则这样的四边形为凹四边形.延长线的同一旁,则这样的四边形为凹四边形.4)四边形的角、对角线及作用四边形的角四边形的对角线ABCDCABD3.四边形的内角和等于多少度?问题:∠A+∠B+∠C+∠D=?CABD四边形的内角和定理:四边形的内角和定理:四边形的内角和等于四边形的内角和等于36360°0°..CABD关于四边形的内角和定理,关于四边形的内角和定理,你能想出其它证明方案吗?你能想出其它证明方案吗?ABCDO注意:注意:研究四边形时,常作它的对角线,把四边形问题转化为三角形问题.4.例题已知:如图,直线OBAB⊥,垂足为B,直线OCAC⊥,垂足为C.求证:(1)1∠+∠A=180°;(2)∠A=∠2.12ABCO12ABCO已知:如图,直线OBAB⊥,垂足为B,直线OCAC⊥,垂足为C.求证:(1)1∠+∠A=180°;(2)∠A=∠2.证明:(1) ∠A+∠ACO+∠1+∠ABO=360°,∴∠1+∠A=360°-90°-90°=180°(四边形的内角和等于(四边形的内角和等于360°360°))(2)1 ∠+∠A=180°,∠1+∠2=180°,∴∠A=∠2. OBABOCAC⊥⊥∴∠ACO=∠ABO=90°,练习1.已知:如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠B,DF平分∠D.问BE与DF是否平行?为什么?A...