北京课改初中数学九下《28.2数学应用举例》PPT课件.pptVIP免费

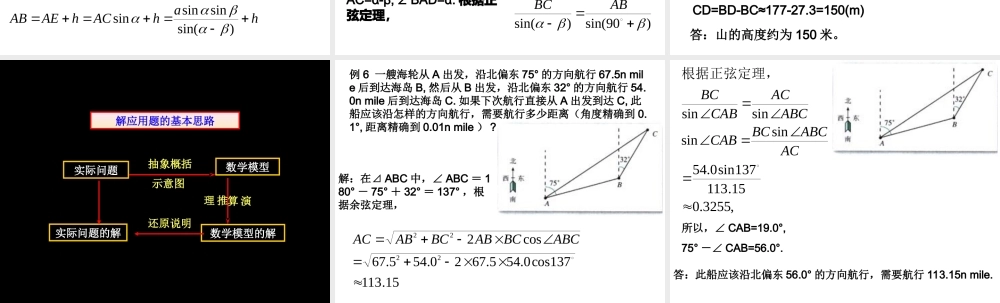
高度角度距离例1．自动卸货汽车的车厢采用液压机构。设计时需要计算油泵顶杆BC的长度．已知车厢的最大仰角是60°，油泵顶点B与车厢支点A之间的距离为1.95m，AB与水平线之间的夹角为6°20’，AC长为1.40m，计算BC的长（精确到0.01m）．0260（1）什么是最大仰角？最大角度最大角度最大角度最大角度（2）例题中涉及一个怎样的三角形？在△ABC中已知什么，要求什么？CAB练习2．自动卸货汽车的车厢采用液压机构。设计时需要计算油泵顶杆BC的长度．已知车厢的最大仰角是60°，油泵顶点B与车厢支点A之间的距离为1.95m，AB与水平线之间的夹角为6°20’，AC长为1.40m，计算BC的长（精确到0.01m）．0260最大角度最大角度最大角度最大角度已知△ABC中AB＝1.95m，AC＝1.40m，夹角∠CAB＝66°20′，求BC．解：由余弦定理，得571.30266cos40.195.1240.195.1cos222222AACABACABBC)(89.1mBC答：顶杆BC约长1.89m。CAB例2AB是底部B不可到达的一个建筑物，A为建筑物的最高点，设计一种测量建筑物高度AB的方法分析：由于建筑物的底部B是不可到达的，所以不能直接测量出建筑物的高。由解直角三角形的知识，只要能测出一点C到建筑物的顶部A的距离CA,并测出由点C观察A的仰角，就可以计算出建筑物的高。所以应该设法借助解三角形的知识测出CA的长。)sin(sinaAChahAChAEAB)sin(sinsinsin解：选择一条水平基线HG,使H,G,B三点在同一条直线上。由在H,G两点用测角仪器测得A的仰角分别是α，β，CD=a,测角仪器的高是h.那么，在⊿ACD中，根据正弦定理可得例2AB是底部B不可到达的一个建筑物，A为建筑物的最高点，设计一种测量建筑物高度AB的方法变式训练：在山顶铁塔上B处测得地面上一点A的俯角α＝54°40′，在塔底C处测得A处的俯角β＝50°1′。已知铁塔BC部分的高为27.3m，求出山高CD(精确到1m)分析：根据已知条件，应该设法计算出AB或AC的长解：在⊿ABC中，∠BCA=90°+β,∠ABC=90°-α,∠BAC=α-β,∠BAD=α.根据正弦定理，)90sin()sin(ABBC)(177)1504054sin(4054sin150cos3.27)sin(sincossin,''''mBCBADABBDABDRt得解CD=BD-BC≈177-27.3=150(m)答：山的高度约为150米。)sin(cos)sin()90sin(BCBCAB所以，实际问题抽象概括示意图数学模型推理演算数学模型的解实际问题的解还原说明解应用题的基本思路例6一艘海轮从A出发，...