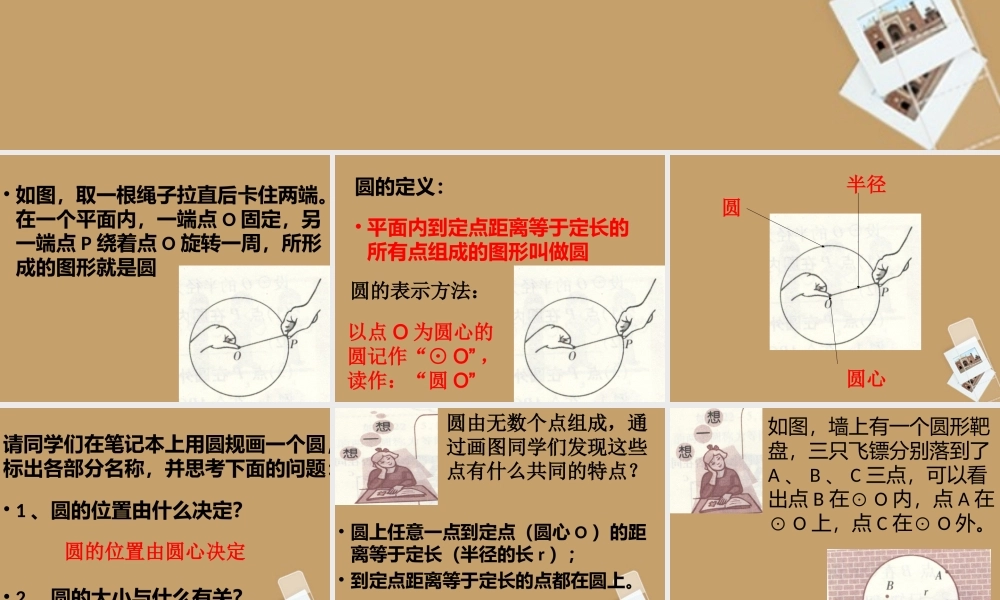
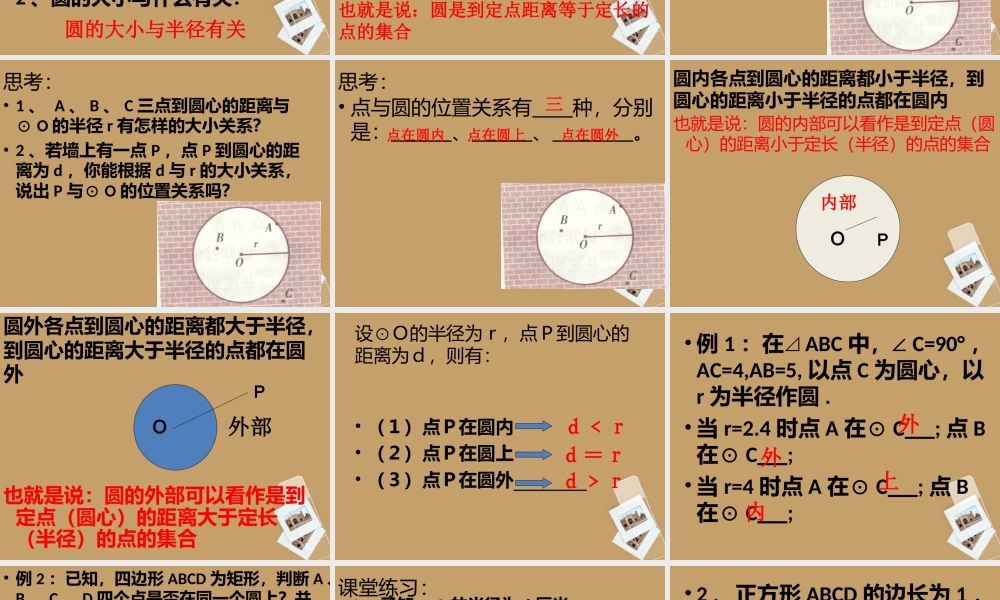
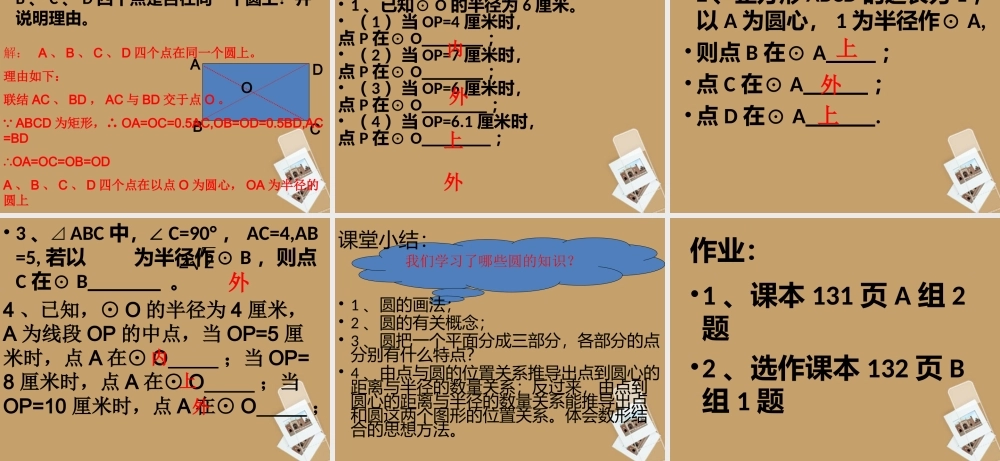
22.1圆的有关概念(一)第二十二章圆•如图,取一根绳子拉直后卡住两端。在一个平面内,一端点O固定,另一端点P绕着点O旋转一周,所形成的图形就是圆圆的定义:•平面内到定点距离等于定长的所有点组成的图形叫做圆圆的表示方法:以点O为圆心的圆记作“⊙O”,读作:“圆O”圆圆心半径请同学们在笔记本上用圆规画一个圆,标出各部分名称,并思考下面的问题:•1、圆的位置由什么决定?•2、圆的大小与什么有关?圆的位置由圆心决定圆的大小与半径有关•圆上任意一点到定点(圆心O)的距离等于定长(半径的长r);•到定点距离等于定长的点都在圆上。圆由无数个点组成,通过画图同学们发现这些点有什么共同的特点?也就是说:圆是到定点距离等于定长的点的集合如图,墙上有一个圆形靶盘,三只飞镖分别落到了A、B、C三点,可以看出点B在⊙O内,点A在⊙O上,点C在⊙O外。思考:•1、A、B、C三点到圆心的距离与⊙O的半径r有怎样的大小关系?•2、若墙上有一点P,点P到圆心的距离为d,你能根据d与r的大小关系,说出P与⊙O的位置关系吗?思考:•点与圆的位置关系有种,分别是:、、。点在圆内点在圆上点在圆外三圆内各点到圆心的距离都小于半径,到圆心的距离小于半径的点都在圆内也就是说:圆的内部可以看作是到定点(圆心)的距离小于定长(半径)的点的集合内部OP圆外各点到圆心的距离都大于半径,到圆心的距离大于半径的点都在圆外也就是说:圆的外部可以看作是到定点(圆心)的距离大于定长(半径)的点的集合外部OP设⊙O的半径为r,点P到圆心的距离为d,则有:•(1)点P在圆内•(2)点P在圆上•(3)点P在圆外d﹤rd=rd﹥r•例1:在⊿ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,以r为半径作圆.•当r=2.4时点A在⊙C;点B在⊙C;•当r=4时点A在⊙C;点B在⊙C;外外上内ABCD•例2:已知,四边形ABCD为矩形,判断A、B、C、D四个点是否在同一个圆上?并说明理由。O解:A、B、C、D四个点在同一个圆上。理由如下:联结AC、BD,AC与BD交于点O。 ABCD为矩形,∴OA=OC=0.5AC,OB=OD=0.5BD,AC=BD∴OA=OC=OB=ODA、B、C、D四个点在以点O为圆心,OA为半径的圆上课堂练习:•1、已知⊙O的半径为6厘米。•(1)当OP=4厘米时,点P在⊙O;•(2)当OP=7厘米时,点P在⊙O;•(3)当OP=6厘米时,点P在⊙O;•(4)当OP=6.1厘米时,点P在⊙O;内外上外•2、正方形ABCD的边长为1,以A为圆心,1为半径作⊙A,•则点B在⊙A;•点C在⊙A;•点D在⊙A.上上外•3...