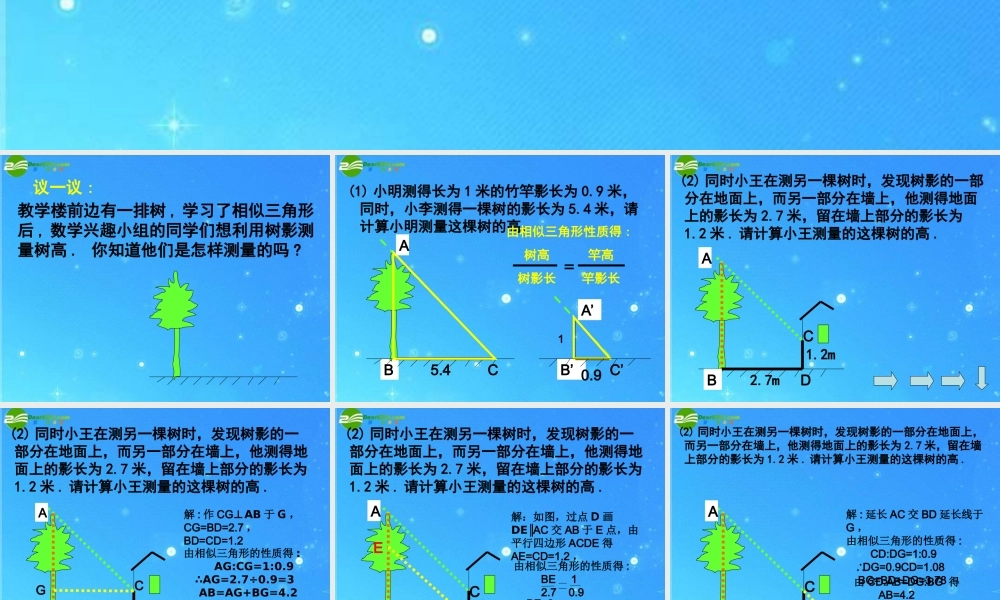
议一议:教学楼前边有一排树,学习了相似三角形后,数学兴趣小组的同学们想利用树影测量树高.你知道他们是怎样测量的吗?BB’(1)小明测得长为1米的竹竿影长为0.9米,同时,小李测得一棵树的影长为5.4米,请计算小明测量这棵树的高.5.40.91由相似三角形性质得:树高竿高树影长竿影长=ACA’C’(2)同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.2.7m1.2mBACD(2)同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.2.7m1.2mBAC解:作CG⊥AB于G,CG=BD=2.7,BD=CD=1.2答:这棵树的高为4.2米.DG由相似三角形的性质得:AG:CG=1:0.9∴AG=2.7÷0.9=3AB=AG+BG=4.2由相似三角形的性质得:BE12.70.9(2)同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.2.7m1.2m解:如图,过点D画DEAC∥交AB于E点,由平行四边形ACDE得AE=CD=1.2,BADCE∴BE=3,AB=BE+AE=4.2答:这棵树高有4.2米.(2)同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.2.7m1.2mBAC解:延长AC交BD延长线于G,由相似三角形的性质得:CD:DG=1:0.9DG=0.9CD=1.08∴BG=BD+DG=3.78由CD:AB=DG:BG得AB=4.2答:这棵树的高为4.2米.DG10mBACD4m30°(3)小明测得长为1米的竹竿影长为2米,同时,小李测量一棵树时发现树影的一部分在地面上,另一部分在斜坡的坡面上,测得在地面影长为10米,在斜坡上影长为4米,斜坡的倾斜角为30°,请计算这棵树的高.10mBAC解:画CG⊥AB于G点,画CE⊥BD于E,则CE=CD=2,DE=2∴BG=CE=2,BE=BD+DE=10+2答:这棵树的高为(7+)米DG由相似三角形的性质得:AG:GC=1:2∴AG=5+AB=BG+AG=7+4mE30°(3)小明测得长为1米的竹竿影长为2米,同时,小李测量一棵树时发现树影的一部分在地面上,另一部分在斜坡的坡面上,测得在地面影长为10米,在斜坡上影长为4米,斜坡的倾斜角为30°,请计算这棵树的高.(3)小明测得长为1米的竹竿影长为2米,同时,小李测量一棵树时发现树影的一部分在地面上,另一部分在斜坡的坡面上,测得在地面影长为10米,在斜坡上影长为4米,斜坡的倾斜角为3...