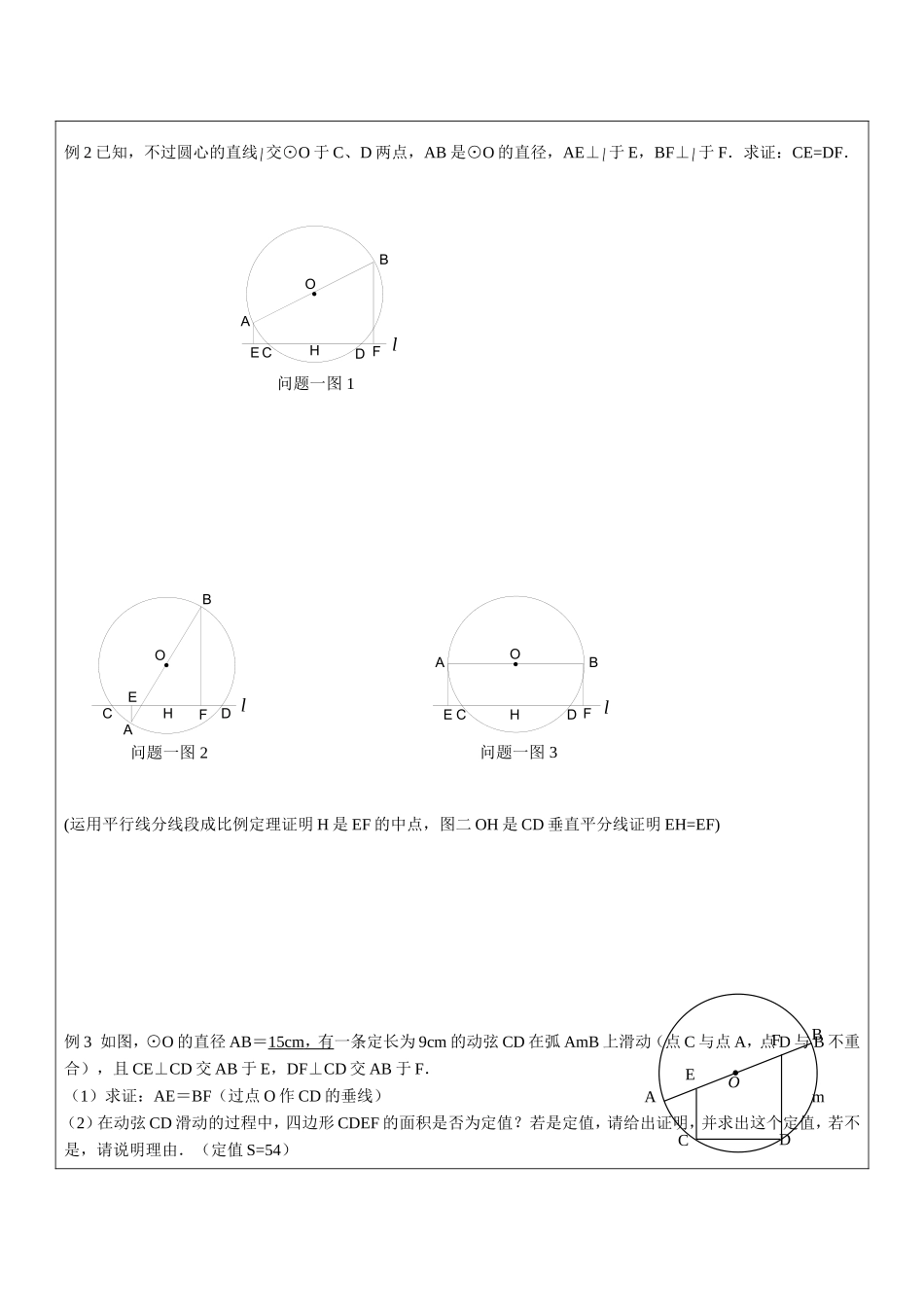
课题垂径定理及其推论教学目标垂径定理的内容及其推论重点、难点垂径定理的内容及其推论考点及考试要求会灵活运用垂径定理的内容及其推论计算及证明。教学内容一、知识点梳理垂径定理:垂直于弦的直径,并且.推论1:①平分弦(不是)的直径,并且.②弦的经过,并且.③平分弦所对的一条孤的直径,,并且.推论2.圆的两条平行弦.垂径定理及推论1中的三条可概括为:①经过;②垂直于;③平分(不是直径);④平分弦所对的;⑤平分弦所对的.以上五点已知其中的任意两点,都可以推得其它两点【典型例题】例1如图AB.CD是⊙O的弦,M.N分别是AB.CD的中点,且.求证:AB=CD.(联结OM,ON)ABDCO·NM例2已知,不过圆心的直线交⊙O于C、D两点,AB是⊙O的直径,AE⊥于E,BF⊥于F.求证:CE=DF.l问题一图1OHFEDCBAl问题一图2OHFEDCBAl问题一图3OHFEDCBA(运用平行线分线段成比例定理证明H是EF的中点,图二OH是CD垂直平分线证明EH=EF)例3如图,⊙O的直径AB=15cm,有一条定长为9cm的动弦CD在弧AmB上滑动(点C与点A,点D与B不重合),且CE⊥CD交AB于E,DF⊥CD交AB于F.(1)求证:AE=BF(过点O作CD的垂线)(2)在动弦CD滑动的过程中,四边形CDEF的面积是否为定值?若是定值,请给出证明,并求出这个定值,若不是,请说明理由.(定值S=54)OABCDEFm例4如图,在⊙O内,弦CD与直径AB交成角,若弦CD交直径AB于点P,且⊙O半径为1,试问:是否为定值?若是,求出定值;若不是,请说明理由.(联结OC,过点O作CD的垂线,定值等于2)【课堂练习】1.已知⊙O的半径为2cm,弦AB长,则这条弦的中点到弦所对劣孤的中点的距离为().A.1cmB.2cmC.D.2.如图1,⊙O的半径为6cm,AB.CD为两弦,且AB⊥CD,垂足为点E,若CE=3cm,DE=7cm,则AB的长为()A.10cmB.8cmC.D.3.有下列判断:①直径是圆的对称轴;②圆的对称轴是一条直径;③直径平分弦与弦所对的孤;④圆的对称轴有无数条.其中正确的判断有()A.0个B.1个C.2个D.3个4.如图2,同心圆中,大圆的弦交AB于C.D若AB=4,CD=2,圆心O到AB的距离等于1,那么两个同心圆的半径之比为()A.3:2B.:2C.:D.5:4ADECB·O图1A·OCDB图2ABCDPO..ABDCO8005.等腰三角形腰长为4cm,底角为,则外接圆直径为()A.2cmB.4cmC.6cmD.8cm6.如图,⊙O的直径为10,弦AB=8,P是弦AB上的一个动点,那么OP长的取值范围是.7.如图,已知有一圆弧形拱桥,拱的跨度AB=16cm,拱高CD=4cm,那么拱形的半径是____m.8.如图,直径为...