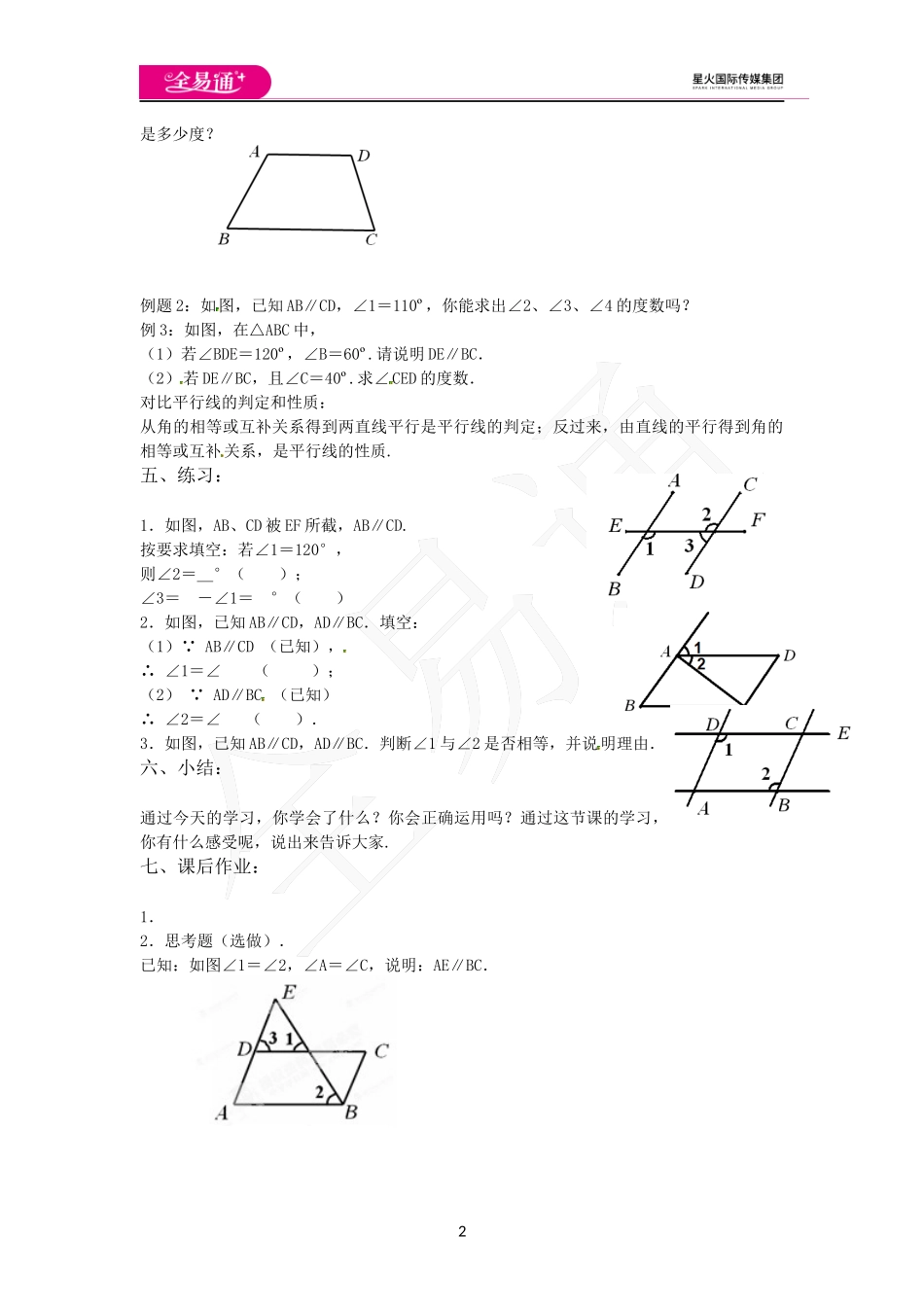
17.2探索平行线的性质第2课时教学目标:1.了解平行线的性质,并能运用它进行简单的运算和证明,能够运用“两直线平行,同位角相等”这一基本事实证明平行线的性质(两直线平行,内错角相等;两直线平行,同旁内角互补);2.掌握相关图形语言、文字语言、符号语言及其互换;3.在定理的探索中锻炼观察能力,并尝试与他人合作开展讨论、研究,并表达自己的见解;4.在观察——实验——猜想——证明的过程中体验探索的方法,逐步形成严谨的思维品质.教学重点:探究平行线的性质教学难点:平行线的性质与判定的区别与联系.教学过程:一、新课引入——情景导入:小明沿正北方向走到A点,向左转50º行进到B点,为了保证继续行进的方向与开始时平行,小明应向哪个方向转多少度?二、复习提问(1)判定两直线平行的方法有哪些?怎样用符号语言表述?(2)若两直线平行,那么同位角有什么关系呢?三、探究新知实验猜想:既然同学们知道两条平行线被第三条直线所截,同位角相等,那么两条平行线被第三条直线所截,内错角、同旁内角各有什么关系呢?利用“几何画板”制作的课件的动画演示初步得出“两直线平行,同位角相等”“两直线平行,同旁内角互补”.四、例题:例题1:例1如图是梯形上底的一部分,已经量得∠A=115°,∠D=100°,梯形另外两个角各ECA1234ABCDE2是多少度?例题2:如图,已知AB∥CD,∠1=110º,你能求出∠2、∠3、∠4的度数吗?例3:如图,在△ABC中,(1)若∠BDE=120º,∠B=60º.请说明DE∥BC.(2)若DE∥BC,且∠C=40º.求∠CED的度数.对比平行线的判定和性质:从角的相等或互补关系得到两直线平行是平行线的判定;反过来,由直线的平行得到角的相等或互补关系,是平行线的性质.五、练习:1.如图,AB、CD被EF所截,AB∥CD.按要求填空:若∠1=120°,则∠2=_°();∠3=-∠1=°()2.如图,已知AB∥CD,AD∥BC.填空:(1)∵AB∥CD(已知),∴∠1=∠();(2)∵AD∥BC(已知)∴∠2=∠().3.如图,已知AB∥CD,AD∥BC.判断∠1与∠2是否相等,并说明理由.六、小结:通过今天的学习,你学会了什么?你会正确运用吗?通过这节课的学习,你有什么感受呢,说出来告诉大家.七、课后作业:1.2.思考题(选做).已知:如图∠1=∠2,∠A=∠C,说明:AE∥BC.3