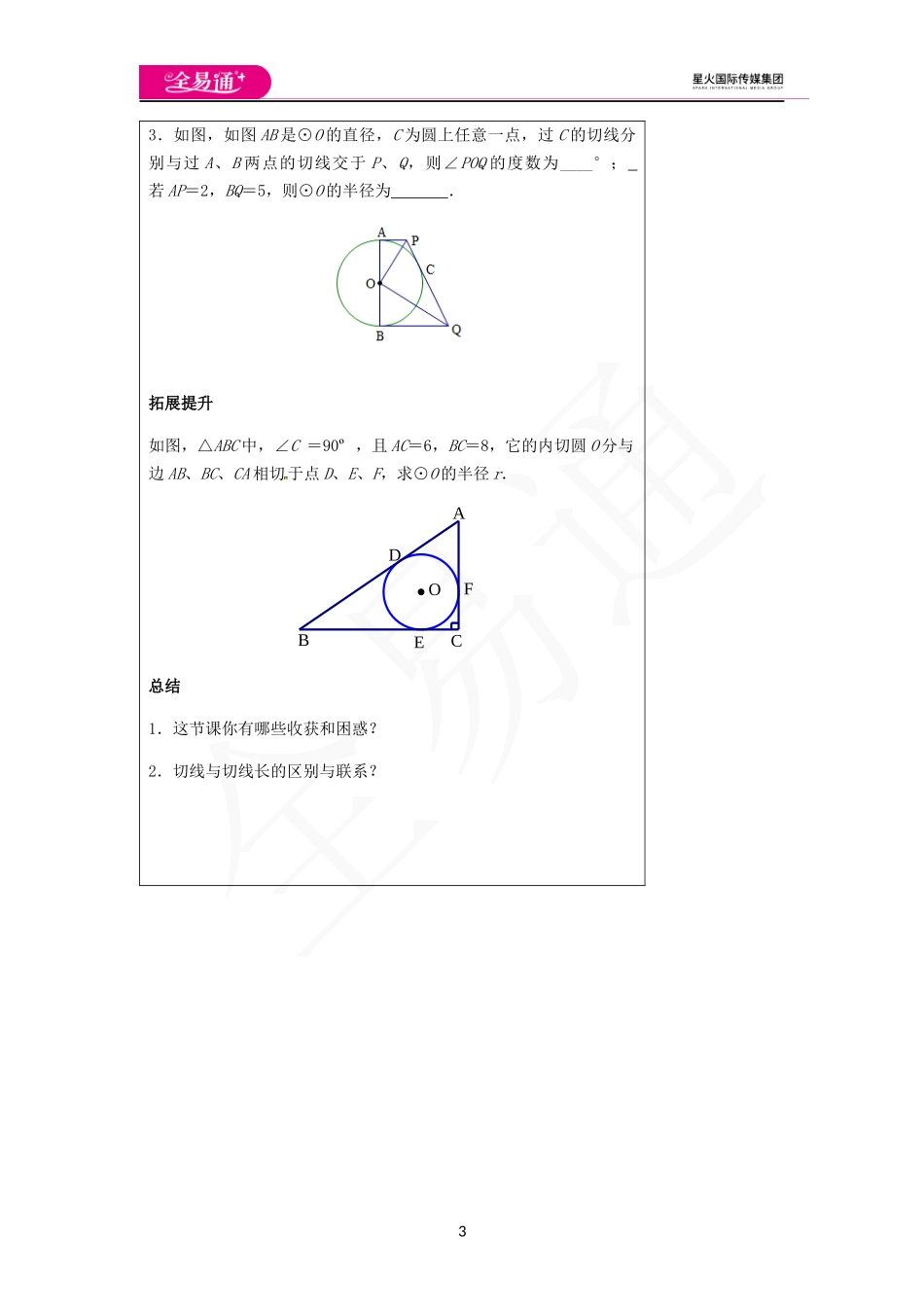
12.5直线与圆的位置关系(4)教学目标【知识与能力】了解切线长的概念.【过程与方法】经历探索切线长性质的过程,并运用这个性质解决问题【情感态度价值观】进一步提高学生的归纳和作图的能力.教学重难点【教学重点】掌握三角形内切圆的画法、理解三角形内切圆的有关概念.【教学难点】通过探索切线长的性质,提高逻辑推理能力.课前准备无教学过程复习引入经过平面上一个已知点,作已知圆的切线会有怎样的情形?1.点在圆内;2.点在圆上;3.点在圆外.实践探索一:切线长的概念1.在经过圆外一点的切线上,这一点和切点之间的线段的长叫做这点到圆的切线长.2.让学生说说:切线与切线长的区别与联系.实践探索二:切线长的性质操作探究:1.如图,若从⊙O外的一点引两条切线PA、PB,切点分别是A、B,连接OA、OB、OP,你能发现什么结论?并证明你所发现的结论.22.请你思考一下:切线长有哪些性质?试用文字语言叙述你所发现的结论.例题讲解例1如图,在以点O为圆心的两个同心圆中,大圆的弦AB、AC分别与小圆相切于点D、E.AB与AC相等吗?为什么?拓展:如果AB、AC是任意两条与小圆相切的弦,那么AB与AC相等吗?例2如图,PA、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切线,切点为C,交PA、PB于点E、F.①已知PA=12cm,求△PEF的周长;②已知∠P=40°,求∠EOF的度数.练一练1.如图,AB、AC、BD是⊙O的切线,切点分别为P、C、D.如果AB=5,AC=3.则BD的长为.2.如图,P是⊙O外一点,PO交⊙O于点C,PC=OC,PA、PB是⊙O的切线,切点分别为A、B.如果⊙O的半径为5,则切线长为,两条切线的夹角为°.FEOPCBA33.如图,如图AB是⊙O的直径,C为圆上任意一点,过C的切线分别与过A、B两点的切线交于P、Q,则∠POQ的度数为____°;若AP=2,BQ=5,则⊙O的半径为.拓展提升如图,△ABC中,∠C=90º,且AC=6,BC=8,它的内切圆O分与边AB、BC、CA相切于点D、E、F,求⊙O的半径r.总结1.这节课你有哪些收获和困惑?2.切线与切线长的区别与联系?FEODCBA