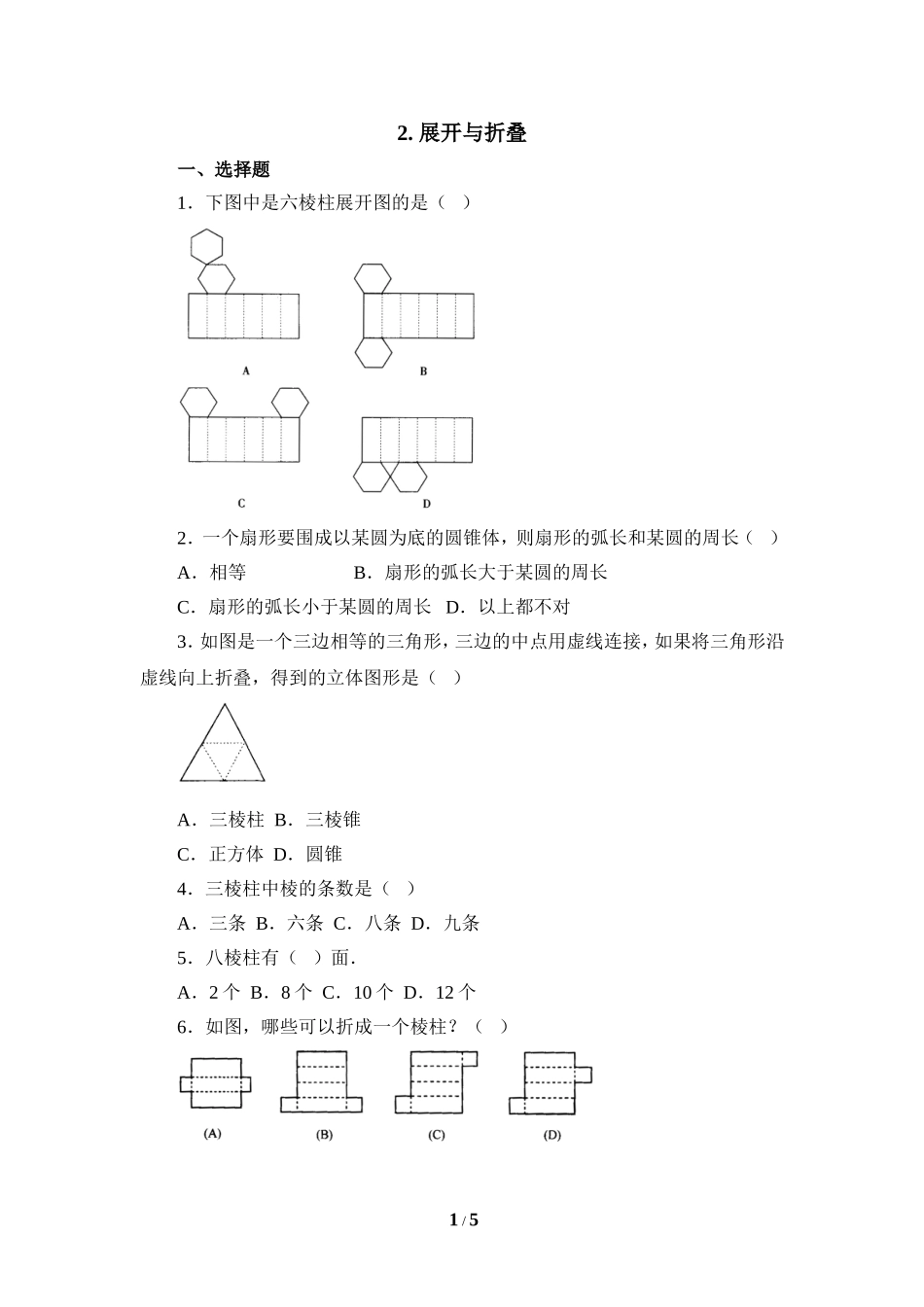
2.展开与折叠一、选择题1.下图中是六棱柱展开图的是()2.一个扇形要围成以某圆为底的圆锥体,则扇形的弧长和某圆的周长()A.相等B.扇形的弧长大于某圆的周长C.扇形的弧长小于某圆的周长D.以上都不对3.如图是一个三边相等的三角形,三边的中点用虚线连接,如果将三角形沿虚线向上折叠,得到的立体图形是()A.三棱柱B.三棱锥C.正方体D.圆锥4.三棱柱中棱的条数是()A.三条B.六条C.八条D.九条5.八棱柱有()面.A.2个B.8个C.10个D.12个6.如图,哪些可以折成一个棱柱?()1/57.如图,把左边的图形折叠起来,它会变成右边的正方体()8.将下图中左边的图形折叠起来围成一个正方体,应该得到右图中的()二、填空题1.七棱柱有____个顶点,有____条棱,有______个侧面.2.圆锥体的底面是_________形,圆锥体的侧面的平面展开图是_______形.3.在图中是正方体展开图的有_________.4.请自己动手用硬纸板剪一个三边都相等的三角形,再用这个三角形围成一个几何体.围成的几何体有_____个面,所有的面都是______形,有______个顶点,_______条棱.其中棱长是原三角形边长的_______.5.一个圆形薄铁,刚好做成两个无底圆锥形容器,则这个圆形薄铁的周长恰好是无底圆锥底面周长的________.6.如图,圆中阴影部分可以是________体侧面的展开平面图.2/5三、判断题1.如图中,①是②的表面展开图.()2.长方体的表面展开图只有一种.()3.由于圆锥体可以由直角三角形旋转得到,所以圆锥体的侧面展开图也可以是三角形.()4.圆锥体的侧面展开图只有一种.()四、解答题1.底面是三角形,四边形的棱柱各有多少条棱?2.想一想,再折一折,下面两图经过折叠能否围成棱柱?3.将图甲(A)中的平面图形按图甲(B)所示的方法折叠,能得到什么样的空间图形?图乙(A)按图乙(B)所示的方法折叠呢?4.如图,右图是左图表面的展开图,右图已有两个面标出是长方体的下面和右面,请你在右图中把长方体的其他面标出来.3/55.请你举出利用圆柱体、长方体的表面能展开成平面图形的原理,在生产和生活中做圆柱形和长方体用品的实例.4/5参考答案一、1.B2.A3.B4.D5.C6.B,C,D.7.B.8.D.二、1.14、21、72.圆、扇3.②、④4.4、三角形、4、6、5.2倍6.圆锥.三、1.×2.×3.×4.√四、1.9,12.2.A能,B不能.3.正方体,四棱锥(你可以用自己的语言描述这个几何体).4.5.圆柱形水桶、长方体包装盒.5/5