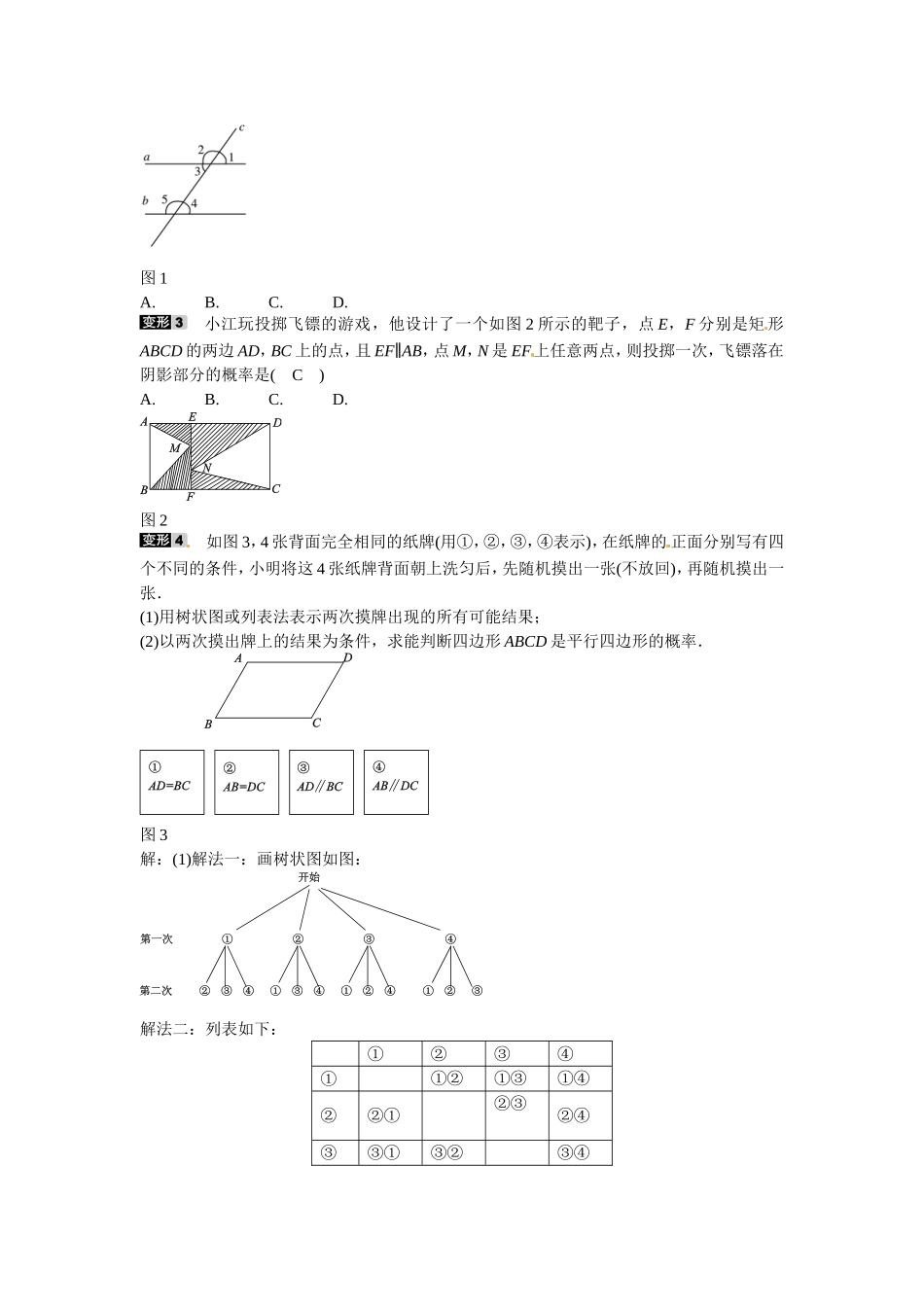
概率与代数、几何知识的综合[见B本P56](教材P141习题25.2第9题)盒中有x枚黑棋和y枚白棋,这些棋除颜色外无其他差别.(1)从盒中随机取出一枚棋子,如果它是黑棋的概率是,写出表示x和y关系的表达式.(2)往盒中再放进10枚黑棋,取得黑棋的概率变为,求x和y的值.解:(1) 从盒中随机地取出一个棋子是黑色棋子的概率是,∴=,y=x.①(2) 如果往盒中再放进10颗黑色棋子,则取得黑色棋子的概率变为,∴=.②由①②解得【思想方法】概率与代数、几何的综合运用其本质还是求概率,只不过应用代数和几何的方法确定某些限制条件的事件数.一般的方法是利用列表或树状图求出所有等可能的情形,再求出满足所涉及知识的情形,进一步求概率,此类问题能很好地考查学生对概率与其他知识的综合运用.一概率与代数的综合有三张正面分别写有数字-2,-1,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为x的值,放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面数字作为y的值,两次结果记作(x,y).(1)用树状图或列表法表示(x,y)所有可能出现的结果;(2)求使分式+有意义的(x,y)出现的概率;(3)化简分式+,并求使分式的值为整数的(x,y)出现的概率.解:(1)画树状图如下:或列表如下:第一次第二次-2-11-2(-2,-2)(-1,-2)(1,-2)-1(-2,-1)(-1,-1)(1,-1)1(-2,1)(-1,1)(1,1)∴所有可能出现的结果为(-2,-2),(-2,-1),(-2,1),(-1,-2),(-1,-1),(-1,1),(1,-2),(1,-1),(1,1).(2)要使分式+有意义,则有(x+y)(x-y)≠0,只有(-2,-1),(-2,1),(-1,-2),(1,-2)符合条件,∴使分式+有意义的(x,y)出现的概率为.(3)+=+=+====,将符合条件的(-2,-1),(-2,1),(-1,-2),(1,-2)分别代入上式计算可得原式=,3,-,-3,∴使分式的值为整数的(x,y)出现的概率为.二概率与几何的综合如图1,直线a//b,直线c与a,b都相交,从所标识的∠1,∠2,∠3,∠4,∠5这五个角中任意选取两个角,则所选取的两个角是互为补角的概率是(A)图1A.B.C.D.小江玩投掷飞镖的游戏,他设计了一个如图2所示的靶子,点E,F分别是矩形ABCD的两边AD,BC上的点,且EF∥AB,点M,N是EF上任意两点,则投掷一次,飞镖落在阴影部分的概率是(C)A.B.C.D.图2如图3,4张背面完全相同的纸牌(用①,②,③,④表示),在纸牌的正面分别写有四个不同的条件,小明将这4张纸牌背面朝...