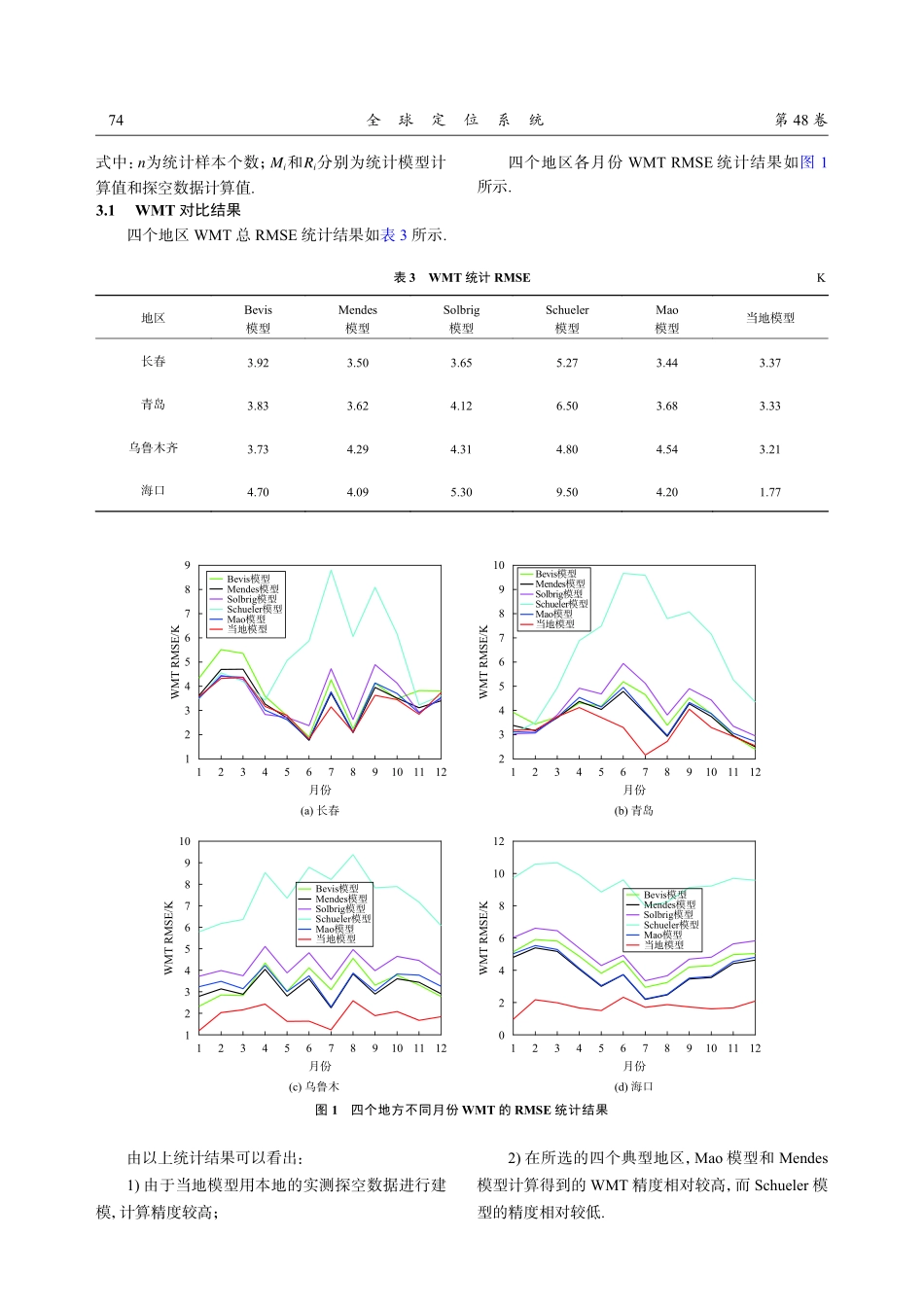
DOI:10.12265/j.gnss.2023016不同加权平均温度模型对大气可降水量影响分析陈祥明1,王宝宝2,李若瑜1,林乐科1,朱庆林1(1.中国电波传播研究所,山东青岛266107;2.航天系统部装备部军事代表局驻石家庄军事代表室,石家庄050081)摘要:加权平均温度(WMT)是地基全球卫星导航系统(GNSS)气象学中解算大气可降水量(PWV)时的一个重要物理量,利用国内四个典型地区2019年的历史气象探空数据计算各剖面的WMT,构建了适合当地的WMT线性统计模型,并对所建模型、工程上常用的几种WMT统计模型及利用其换算得到的PWV进行了对比.根据统计结果可知:对于精度较高的需求,构建适合当地的统计模型是很有必要的,另外,各统计模型中Mao模型和Mendes模型的精度相对较高,在不具备建模条件的情况下可以优先考虑.本统计结果可为其他涉及WMT的工程应用提供参考.关键词:地基全球卫星导航系统(GNSS)气象学;大气可降水量(PWV);加权平均温度(WMT);对流层天顶湿延迟(ZWD);转换因子中图分类号:P228.4;TN011文献标志码:A文章编号:1008-9268(2023)03-0072-050引言水汽是重要的温室气体,其随时空的变化对气象预报、气候变化以及水循环等研究均有重要的意义,利用地基全球卫星导航系统(GNSS)获取对流层延迟来反演大气可降水量(PWV)是GNSS气象学的重要研究内容.基于GNSS载波相位观测值、高精度卫星星历和卫星钟差,利用精密单点定位(PPP)算法[1]解算对流层总天顶延迟(ZTD),而对流层静力延迟(ZHD)可利用地面气象参数较精确的获得[2].ZTD扣除ZHD,即得到对流层天顶湿延迟(ZWD).PWV可由ZWD进一步换算得到,而加权平均温度(WMT)是转换因子的一个重要影响因素[3].本文选择国内四个典型地区,利用2019年当地的历史气象探空数据(常规气象探测为每天两组气象探空数据,时间分别为0:00UT和12:00TU),用数值积分的方式计算所有剖面的WMT,构建了适合当地的WMT线性统计模型;对比了该统计模型以及其他常用的WMT统计模型换算得到的PWV值,并统计了与利用探空剖面计算的PWV的均方根误差(RMSE).根据统计结果给出工程建议,为其他涉及WMT的工程应用提供了技术参考.1PWV1.1大气折射率湿项计算Nw工程中常用的对流层大气折射率湿项的计算公式为Nw=k′2eT+k3eT2.(1)k′2=k2−k1RdRvk1k2k3k1k2k′2k3k1k2k3RdRvRdRveTtTt式中:,、、为常数,、、单位为K/hPa,的单位为K2/hPa.Thayer[4]给出的参考值分别为=77.604±0.014、=64.79±0.08、=377600±400,和分别为干空气和湿空气的气体常数,=0....