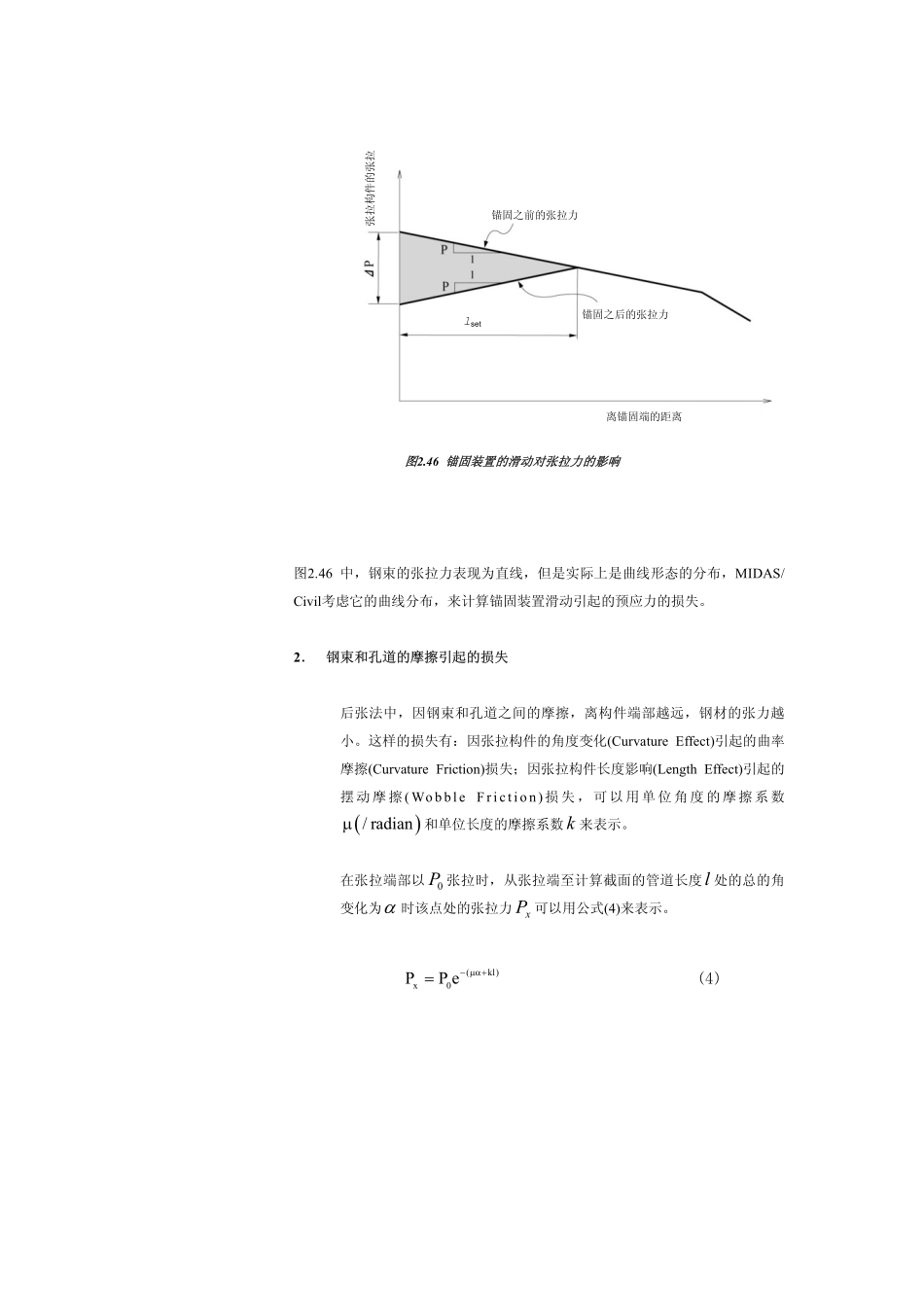
预应力损失随时间的推移,钢束的张拉应力因各种原因变小,这样,作用到混凝土上的预应力也随之变小,其原因如下:�施加预应力时的瞬时损失(IstantaneousLoss)1.锚固装置的滑动(AnchorangeSlip)2.钢束和孔道之间的摩擦3.混凝土的弹性变形(ElasticShortening)�施加预应力以后随时间的推移引起的损失(TimeDependentLoss)1.混凝土的徐变2.混凝土的收缩3.钢束的松弛(Relaxation)后张法考虑上述六种预应力损失原因,但是先张法不考虑钢束和孔道之间的摩擦。预应力的瞬时损失和随时间的推移引起的损失之和达到初始拉力(OriginalJackingForce)的20~30%之多。预应力构件的混凝土应力计算中,最重要的参数为瞬时损失后的拉力iP和随时间推移引起的损失后的最后作用于钢束的拉力eP(EffectivePrestressForce)。iP和eP的关系可以用以下公式表示,eiPRP=其中,R为预应力的有效率(EffectiveRatio),一般来说,先张法为R0.80=,后张法为R0.85=以下是对MIDAS/CIVIL考虑的预应力损失的方法的说明:�瞬时损失1.锚固装置滑动引起的损失钢束的张拉结束后,随锚固装置的不同,锚固端部会有一些滑动。因此钢束的张拉端部附近会发生张力损失,这称为锚固装置滑动引起的损失(或锚具变形和钢筋内缩)。这种损失不仅在后张法中发生,也发生在先张法中。不管是什么方式,都可用张拉作业时的超张应力(Overstressing)来校正。一般来讲,因钢束和孔道之间的存在一定的摩擦,锚固装置的滑动引起的张力的损失只限于锚固装置附近即张拉端部附近,远离张拉端处,几乎没有张力损失的现象。受锚固装置的滑动影响的张拉构件的长度setl是摩擦损失的函数,若摩擦损失越大,其长度越小;摩擦损失越小,其长度越长(图2.46所示)。把滑移量(l∆)、钢材截面积(pA)、弹性模量(pE)三个参数相乘,等于图2.46中的三角形的面积,这样下面等式成立。三角形面积(0.5setPl∆)=ppAEl∆(1)假设张拉构件单位长度的摩擦损失为p,张拉力的损失p∆由图2.46可知,可以表示为2setPpl∆=(2)由式(1)和(2)可以推导出受锚固装置滑动影响的张拉构件的长度()setl的公式,ppsetAEllp∆=(3)锚固之前的张拉力锚固之后的张拉力离锚固端的距离张拉构件的张拉lset图2.46锚固装置的滑动对张拉力的影响图2.46中,钢束的张拉力表现为直线,但是实际上是曲线形态的分布,MIDAS/Civil考虑它的曲线分布,来计算锚固装置滑动引起的预应力的损失。2.钢束和孔道的摩擦引起的损失后张法中,因钢束和孔道之间的摩擦,离构件端部越...