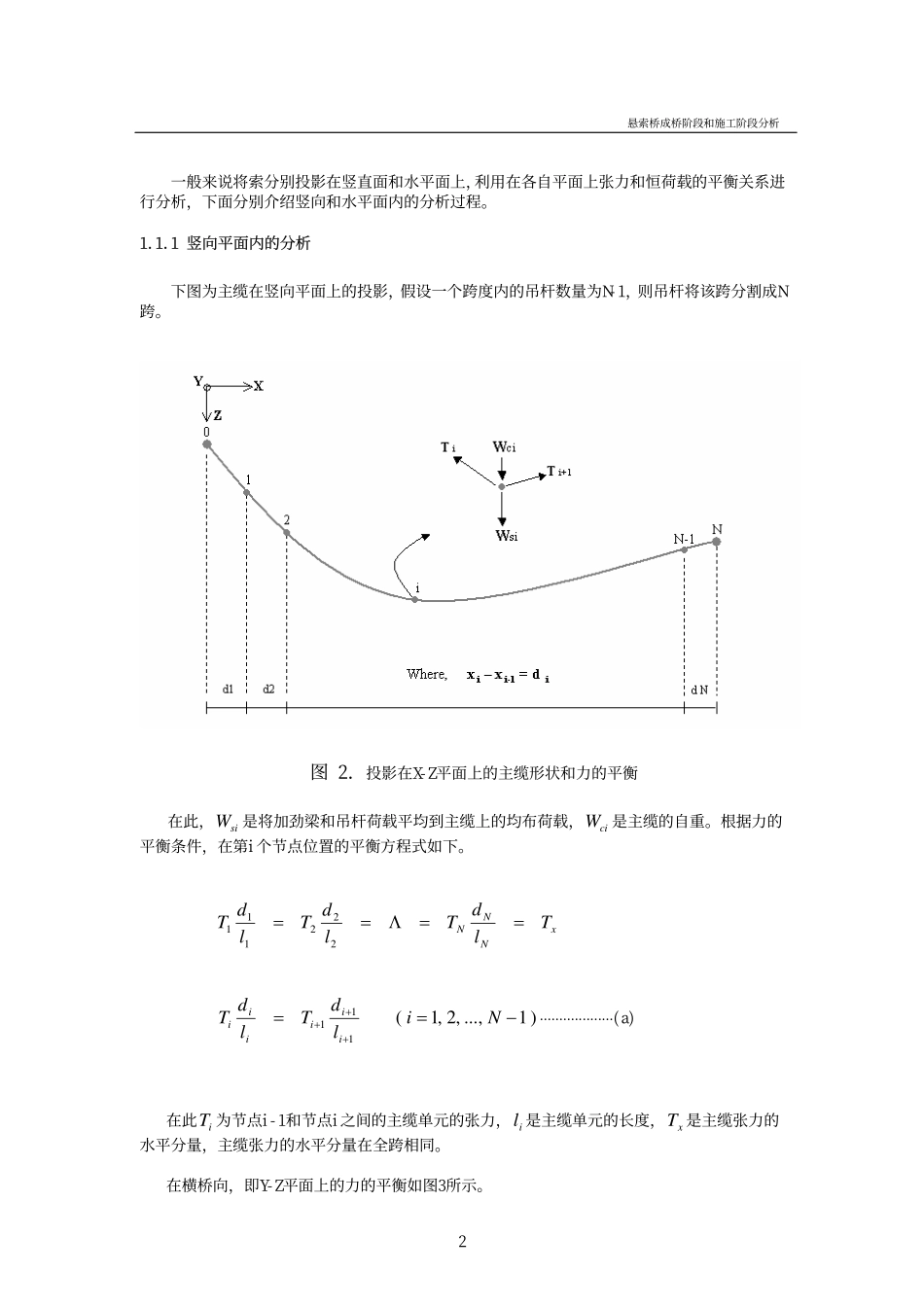
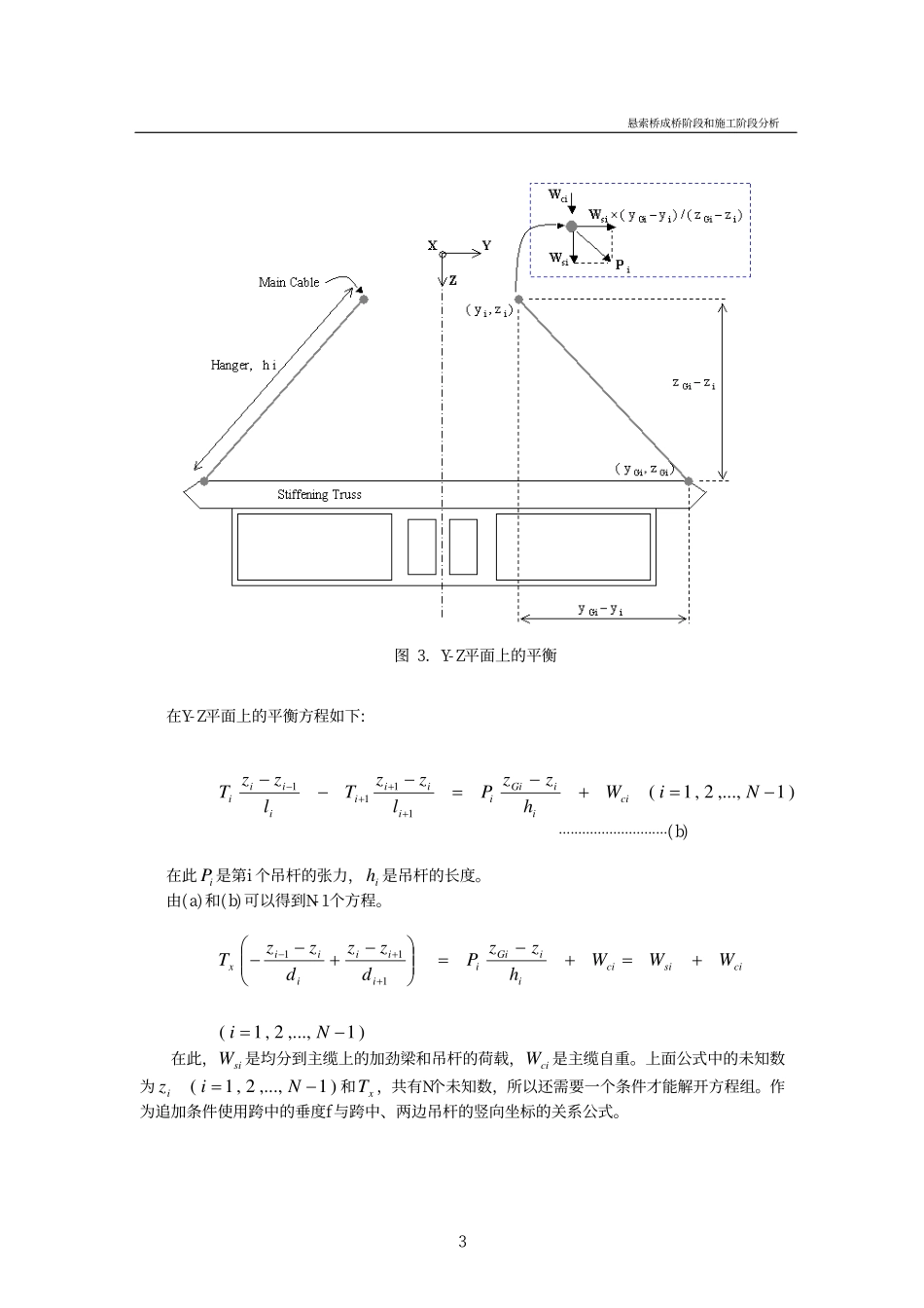
悬索桥成桥阶段和施工阶段分析用MIDAS/Civil做悬索桥分析1.悬索桥初始平衡状态分析理论悬索桥与一般中小跨经桥梁的区别就是悬索桥的自重和大部分施工荷载主要由主缆来承担。特别是成桥后在恒载作用下主缆和吊杆的张力、桥形应与设计目标一致。悬索桥的主缆是变形性很大的承重构件,施工过程中主缆和加劲梁的几何形状变化非常大,所以进行悬索桥设计时,要做逆施工阶段分析(倒拆分析),为了做考虑几何非线性的倒拆分析还需要做自重荷载下的初始平衡状态分析。悬索桥在加劲梁的自重作用下产生变形后达到平衡状态,在满足设计要求的垂度和跨经条件下,计算主缆的坐标和张力的分析一般称为初始平衡状态分析。这是对运营阶段进行线性、非线性分析的前提条件,所以应尽量使初始平衡状态分析结果与设计条件一致。悬索桥的初始平衡状态分析阶段是以悬索桥的基本假定为基础,利用节线法来计算空缆线形的过程。节线法是利用加劲梁、吊杆自重作用下产生的内力平衡条件来计算主缆的坐标和张力的方法。此方法是悬索桥(广安大桥、永宗大桥、日本明石海峡大桥)广泛应用的方法。最近除了节线法之外,还有利用弹性悬链线确定空缆线形的方法和考虑加劲梁、主缆、主塔体系来决定整体结构形状的精确分析的方法。MIDAS/Civil软件不仅能做节线法分析,而且还能对整体结构体系做精确的初始平衡状态分析。1.1节线法该方法采用了日本Ohtsuki博士使用的计算索平衡状态方程式,是利用桥梁自重和主缆张力的平衡方程计算主缆坐标和主缆张力的方法。其基本假定如下:(1)吊杆仅在横桥向倾斜,垂直于顺桥向。(2)主缆张力沿顺桥向分量在全跨相同。(3)假定主缆与吊杆的连接节点之间的索呈直线形状,而非抛物线形状。(4)主缆两端坐标、跨中垂度、吊杆在加劲梁上的吊点位置、加劲梁的恒荷载等为已知量。吊杆间主缆的张力分布如图1所示。图1.主缆张力1悬索桥成桥阶段和施工阶段分析一般来说将索分别投影在竖直面和水平面上,利用在各自平面上张力和恒荷载的平衡关系进行分析,下面分别介绍竖向和水平面内的分析过程。1.1.1竖向平面内的分析下图为主缆在竖向平面上的投影,假设一个跨度内的吊杆数量为N-1,则吊杆将该跨分割成N跨。图2.投影在X-Z平面上的主缆形状和力的平衡在此,是将加劲梁和吊杆荷载平均到主缆上的均布荷载,是主缆的自重。根据力的平衡条件,在第i个节点位置的平衡方程式如下。siWciWxNNNTldTldTldT==Λ==222111)1...,,2,1(111−==+++NildTldTiiiiii⋅⋅⋅⋅⋅⋅⋅...