3.1.1 椭圆及其标准方程（含3课时）（教学课件）-2023-2024学年高二数学同步精品课堂（人教A版2019选择性必修第一册）.pptxVIP免费

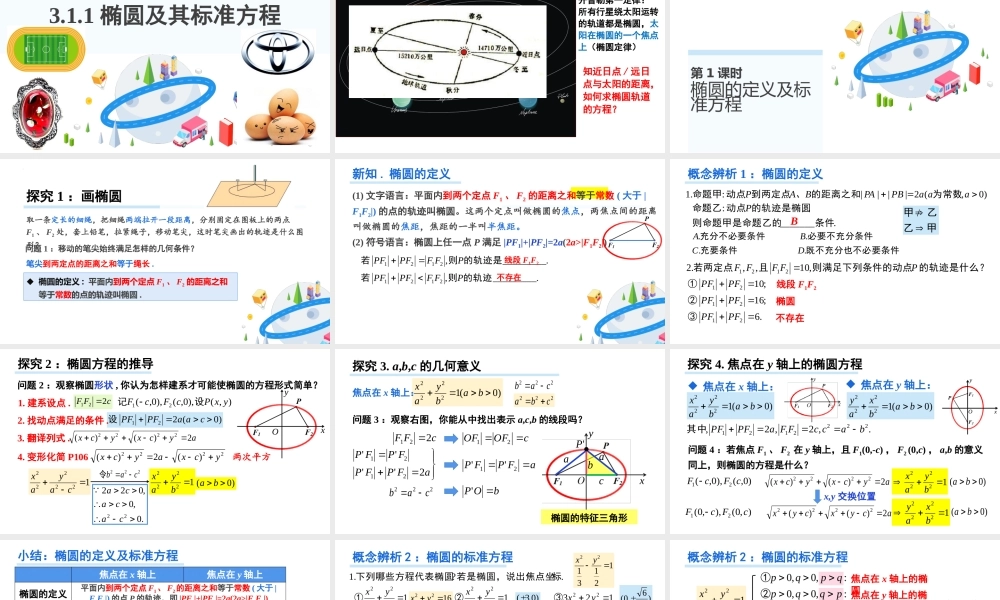
第三章圆锥曲线的方程截圆锥而得到的曲线：圆、椭圆、双曲线、抛物线3.1.1椭圆及其标准方程NoImage开普勒第一定律：所有行星绕太阳运转的轨道都是椭圆，太阳在椭圆的一个焦点上（椭圆定律）知近日点/远日点与太阳的距离，如何求椭圆轨道的方程？第1课时椭圆的定义及标准方程探究1：画椭圆问题1：移动的笔尖始终满足怎样的几何条件？椭圆的定义:平面内到两个定点F1、F2的距离之和等于常数的点的轨迹叫椭圆.笔尖到两定点的距离之和等于绳长.取一条定长的细绳，把细绳两端拉开一段距离，分别固定在图板上的两点F1、F2处，套上铅笔，拉紧绳子，移动笔尖，这时笔尖画出的轨迹是什么图形？._________,2121的轨迹是则若PFFPFPF新知.椭圆的定义(1)文字语言：平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫椭圆。这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距，焦距的一半叫半焦距。线段F1F2._________,2121的轨迹则若PFFPFPF不存在(2)符号语言：椭圆上任一点P满足|PF1|+|PF2|=2a(2a>|F1F2|)._______.:条件则命题甲是命题乙的的轨迹是椭圆动点命题乙P既不充分也不必要条件充要条件必要不充分条件充分不必要条件....DCBAB概念辨析1：椭圆的定义)0,(2||||:.1aaaPBPABAP为常数的距离之和、到两定点动点命题甲的轨迹是什么？则满足下列条件的动点且若两定点PFFFF,10,,.22121.6;16;10212121PFPFPFPFPFPF③②①线段F1F2椭圆不存在甲乙乙甲/探究2：椭圆方程的推导问题2：观察椭圆形状,你认为怎样建系才可能使椭圆的方程形式简单？1.建系设点.cFF221),(),0,(),0,(21yxPcFcF设记)0(221caaPFPF设2.找动点满足的条件.3.翻译列式.aycxycx2)()(22222222)(2)(ycxaycx4.变形化简P106122222cayax.0,0,02222cacaca12222byax222cab令Oxy两次平方)0(ba探究3.a,b,c的几何意义aFPFPFPFP2''''2121cFF221)0(12222babyax问题3：观察右图，你能从中找出表示a,c,b的线段吗？c222cabaFPFP21''abcOFOF21bOP'222cab222cbaa'P椭圆的特征三角形xy焦点在x轴上：探究4.焦点在y轴上的椭圆方程.,2,2,2222121baccFFaPFPF其中)0(12222babyax问题4：若焦点F1、F2在y轴上，且F1(0,-c)，F2(0,c)，a,b的意义同上，则椭圆的方程是什么？焦点在x轴上：焦点在y轴上：acyxcyx2)()(222...