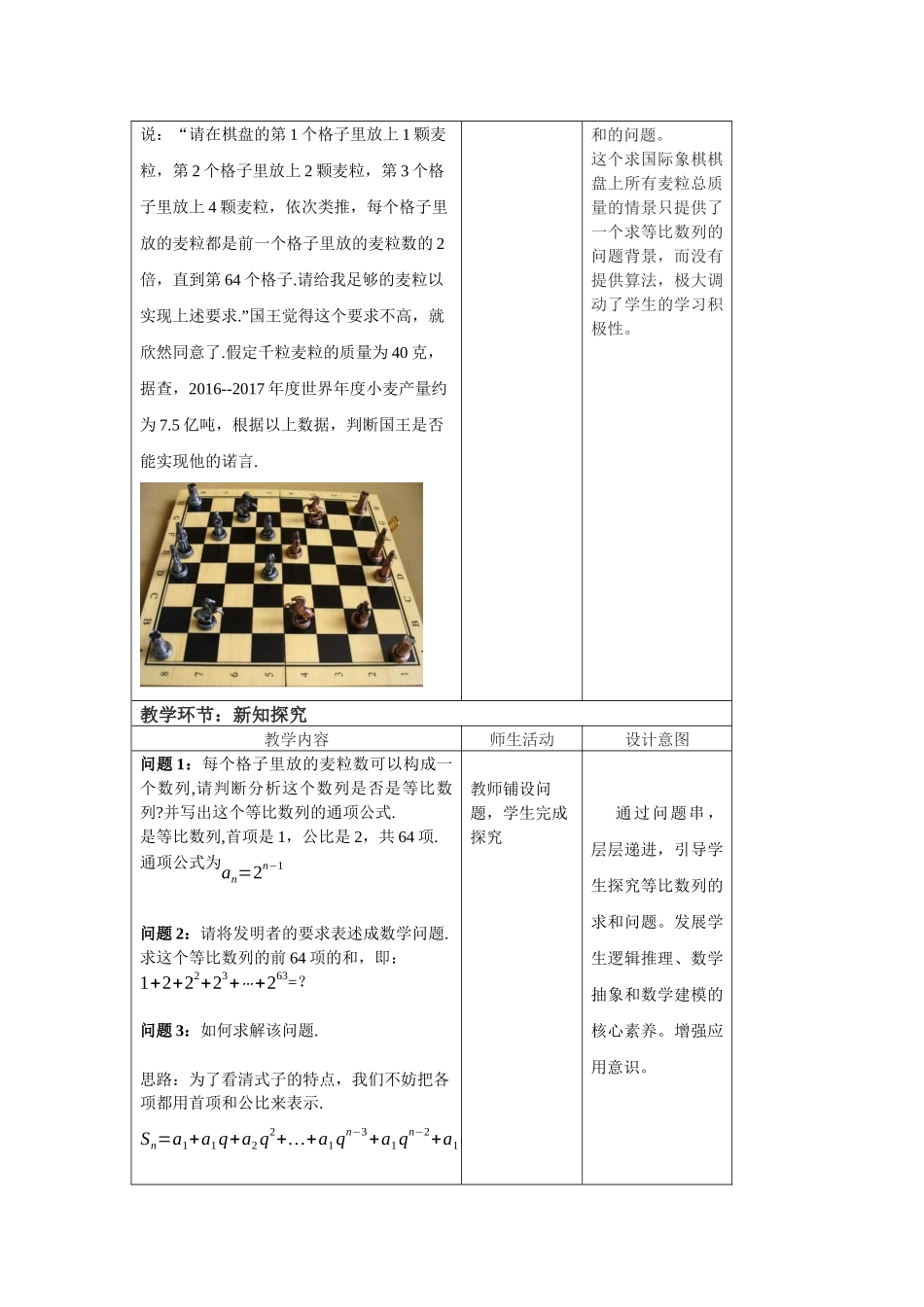
《4.3.2等比数列的前n项和公式(1)》教学设计-------李德峰(一)教学内容等比数列的前n项和公式(二)教材分析1.教材来源本节课选自《2019人教A版高中数学选择性必修二》第四章《数列》2.地位与作用数列是高中代数的主要内容,它与数学课程的其它内容(函数、三角、不等式等)有着密切的联系,又是今后学习高等数学的基础,所以在高考中占有重要地位。(三)学情分析1.认知基础:学生在已学习等差数列前n项和公式的基础上,引导学生类比学习等比数列前n项和公式2.认知障碍:等比数列前n项和公式推导需要突破被等差数列前n项和的思维定势。(四)教学目标1.知识目标:①探索并掌握等比数列的前n项和公式.②解等比数列的通项公式与前n项和公式的关系.2.能力目标:通过公式运用的探索,提高类比与转化的数学能力3.素养目标:在探索等比数列的前n项和公式的过程中,发展学生的数学运算和逻辑推理素养(五)教学重难点:1.重点:等比数列的前n项的运用2.难点:等比数列的前n项和公式的推导(六)教学思路与方法教学过程分为问题呈现阶段、探索与发现阶段、应用知识阶段(七)课前准备多媒体(八)教学过程教学环节:新课引入教学内容师生活动设计意图国际象棋起源于古代印度.相传国王要奖赏国际象棋的发明者,问他想要什么.发明者让学生猜想讨论用一个有趣的故事情景来引入数列求说:“请在棋盘的第1个格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒,依次类推,每个格子里放的麦粒都是前一个格子里放的麦粒数的2倍,直到第64个格子.请给我足够的麦粒以实现上述要求.”国王觉得这个要求不高,就欣然同意了.假定千粒麦粒的质量为40克,据查,2016--2017年度世界年度小麦产量约为7.5亿吨,根据以上数据,判断国王是否能实现他的诺言.和的问题。这个求国际象棋棋盘上所有麦粒总质量的情景只提供了一个求等比数列的问题背景,而没有提供算法,极大调动了学生的学习积极性。教学环节:新知探究教学内容师生活动设计意图问题1:每个格子里放的麦粒数可以构成一个数列,请判断分析这个数列是否是等比数列?并写出这个等比数列的通项公式.是等比数列,首项是1,公比是2,共64项.通项公式为an=2n−1问题2:请将发明者的要求表述成数学问题.求这个等比数列的前64项的和,即:1+2+22+23+⋯+263=?问题3:如何求解该问题.思路:为了看清式子的特点,我们不妨把各项都用首项和公比来表示.Sn=a1+a1q+a2q2+…+a1qn−3+a1qn−2+a1qn−1教师铺设问题...