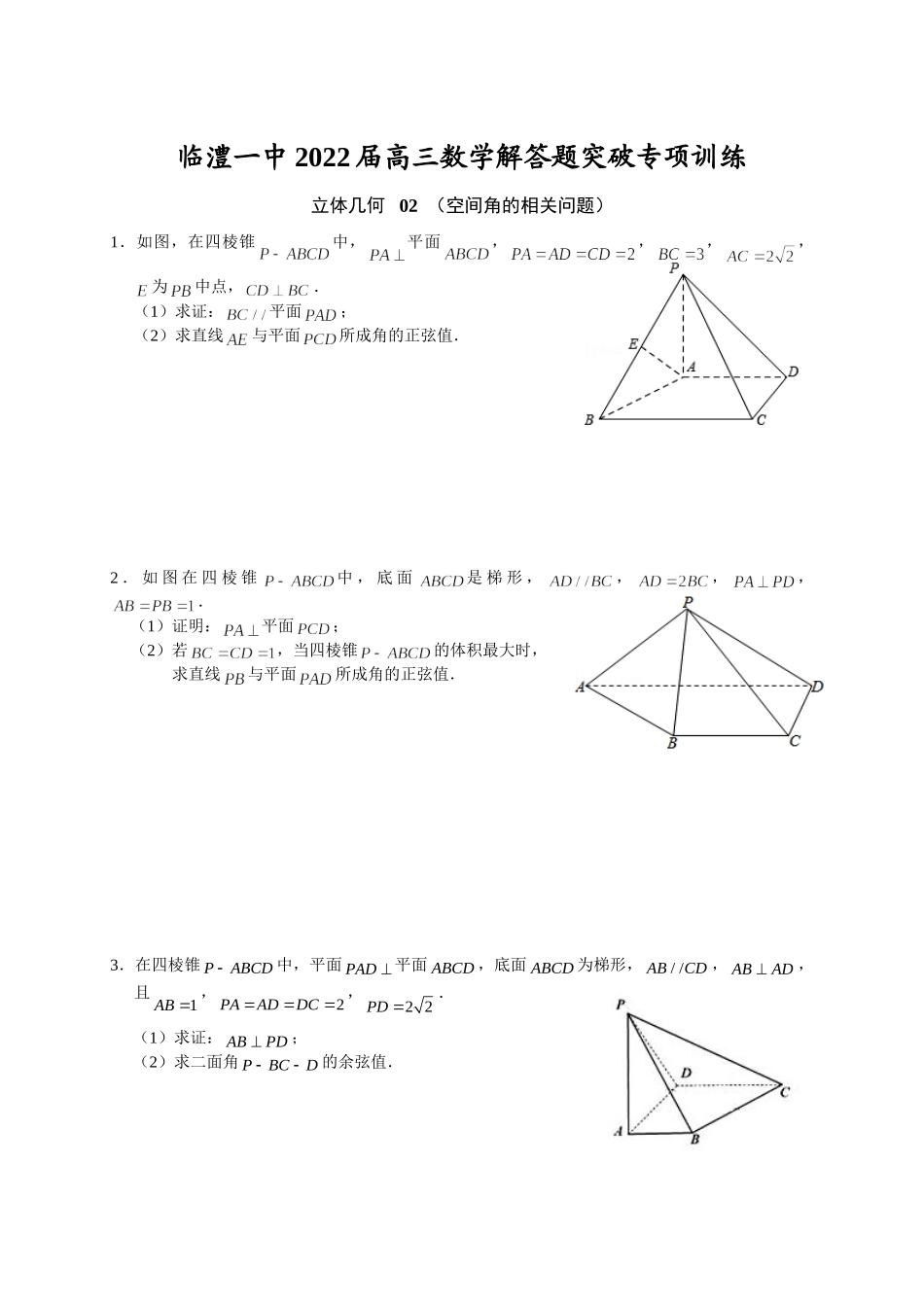
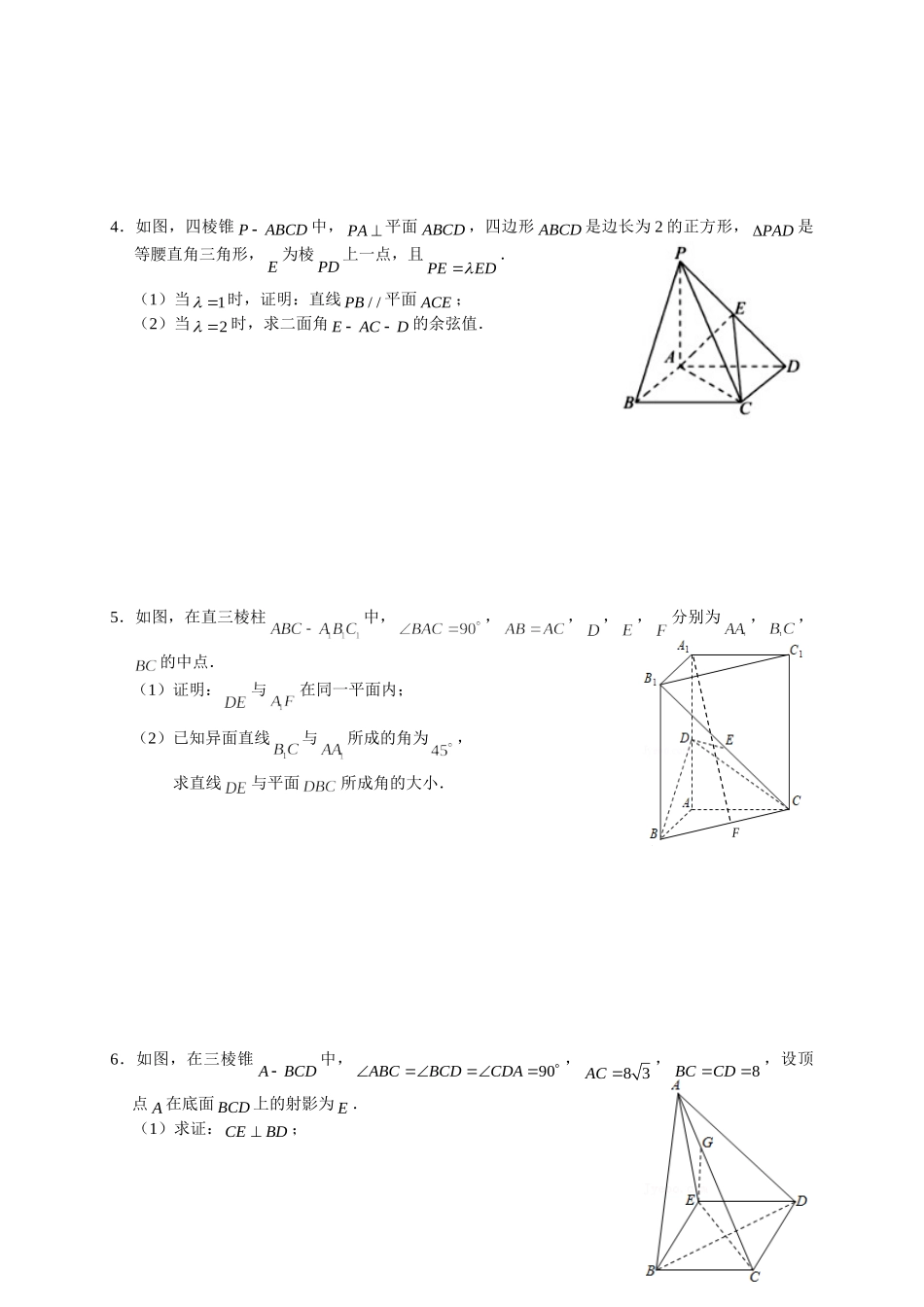
临澧一中2022届高三数学解答题突破专项训练立体几何02(空间角的相关问题)1.如图,在四棱锥中,平面,,,,为中点,.(1)求证:平面;(2)求直线与平面所成角的正弦值.2.如图在四棱锥中,底面是梯形,,,,.(1)证明:平面;(2)若,当四棱锥的体积最大时,求直线与平面所成角的正弦值.3.在四棱锥PABCD中,平面PAD平面ABCD,底面ABCD为梯形,//ABCD,ABAD,且1AB,2PAADDC,22PD.(1)求证:ABPD;(2)求二面角PBCD的余弦值.4.如图,四棱锥PABCD中,PA平面ABCD,四边形ABCD是边长为2的正方形,PAD是等腰直角三角形,E为棱PD上一点,且PEED�.(1)当1时,证明:直线//PB平面ACE;(2)当2时,求二面角EACD的余弦值.5.如图,在直三棱柱中,,,,,分别为,,的中点.(1)证明:与在同一平面内;(2)已知异面直线与所成的角为,求直线与平面所成角的大小.6.如图,在三棱锥ABCD中,90ABCBCDCDA,83AC,8BCCD,设顶点A在底面BCD上的射影为E.(1)求证:CEBD;F(2)设G为棱AC上的一点,且二面角CEGD的余弦值为105,求三棱锥GECD的体积.7.如图,在四棱锥中,平面,底面是直角梯形,其中,,,,为棱上的点,且.(1)若为棱的中点,求证:平面;(2)(ⅰ)求证平面;(ⅱ)设为棱上的点(不与,重合),且直线与平面所成角的正弦值为,求的值.8.如图,在直三棱柱中,,,为的中点.(1)若为上的一点,且,求证:;(2)在(1)的条件下,若异面直线与所成的角为,求直线与平面所成角的余弦值.9.如图,在四棱锥PABCD中,PBC为正三角形,底面ABCD为直角梯形,//ADBC,4BC,90ADC,3ADCD,点M,N分别在线段AD和PC上,且2DMCNAMPN.(1)求证://PM平面BDN;(2)设二面角PBCA大小为,若3cos3,求直线BD和平面PAD所成角的正弦值.参考答案1.(1)证明:因为,,∴,∴.又,∴.又平面且平面,所以平面.(2)过点作的垂线交于点.因为平面,所以,,以点为坐标原点,以,,分别为,,轴建立如图的空间直角坐标系,则,0,,,2,,,2,,,0,,,,.因为为的中点,,,.所以,,,,2,,,2,.设平面的法向量为,,,则,令,得,1,.设直线与平面所成的角为,所以.所以直线与平面所成角的正弦值为.2.(1)证明:取,中点,,连接,,.由,得,,所以平面.又由,知:四边形是平行四边形,则....