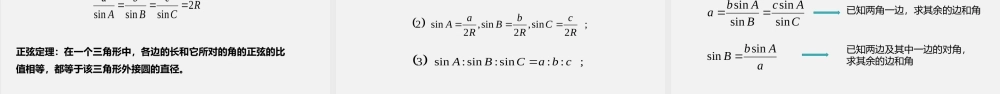9.1.1正弦定理数学(人教B版2019)必修第四册第九章解三角形学习目标1.理解正弦定理的推导过程,掌握正弦定理、三角形的面积公式。2.掌握正弦定理的简单应用,并通过例题熟练掌握正弦定理可解的两类三角形。3.深刻体会从特殊到一般的思维过程,注意分类讨论、数形结合两种重要思想方法的运用。学习重难点学习重点:正弦定理的推导及应用学习难点:三角形边角关系的探究过程和初步运用情境引入陶哲轩,1975年7月17日出生于澳大利亚阿德莱德,华裔数学家,菲尔兹奖获得者、英国皇家学会院士、美国国家科学院外籍院士、美国艺术与科学学院院士,美国加州大学洛杉矶分校JamesandCarolCollins讲席教授、博士生导师。陶哲轩13岁获得国际数学奥林匹克竞赛数学金牌;16岁获得弗林德斯大学学士学位;17岁获得弗林德斯大学硕士学位;21岁获得普林斯顿大学博士学位;24岁起在加利福尼亚大学洛杉矶分校担任教授;2006年31岁时获得菲尔兹奖、拉马努金奖和麦克阿瑟天才奖;2008年获得艾伦·沃特曼奖;2009年12月作为第二届"丘成桐中学数学奖"的评审总决赛的面试主考官来到中国;2015年获得科学突破奖-数学突破奖。陶哲轩的兴趣横跨多个数学领域,包括调和分析、非线性偏微分方程和组合论。被誉为“数学界的莫扎特”。情境引入数学在某方面类似于考古学。你也许会找到某个东西的一角,并由此判断它是有趣的。于是你开始在别处挖掘,又找到了非常相似的另一角,你会想,是否有更深的联系?你继续挖掘,最终发现了地下的结构。当某些东西最终表明有意义时,你有一种发现的激动。陶哲轩:情境引入在现代过程中,得益于科技的发展,距离的测量能借助红外测距仪、激光测距仪等工具直接完成。不过,在这些工具没有出现以前,你知道人们是怎样间接获得不能到达的两点间距离的吗?如图所示,若想知道河对岸的一点A与岸边一点B之间的距离,而且已经测量出了BC的长,也想办法得到了ABC与ACB的大小,你能借助这三个量,求出AB的长吗?抽象出的数学问题是什么样的?BAC为了方便起见,将ABC的3个内角,,ABC所对的边分别记为,,abc,在这样的约定下,情景中的问题可以转化为:已知,,aBC,如何求c.acb能得到结论吗?恰好是直角三角形,你若ABC情境引入公式探究ABCabc.,,,cCBa求问题:已知,,sinsinsin即abccccABCsinsinsin所以abcABC在Rt△ABC中,有ccCcbBcaA1sin,sin,sinCcBbAasinsinsin此结论是否也适用于一般的斜三角形?公式探究公式探究探究方向1:借助于...