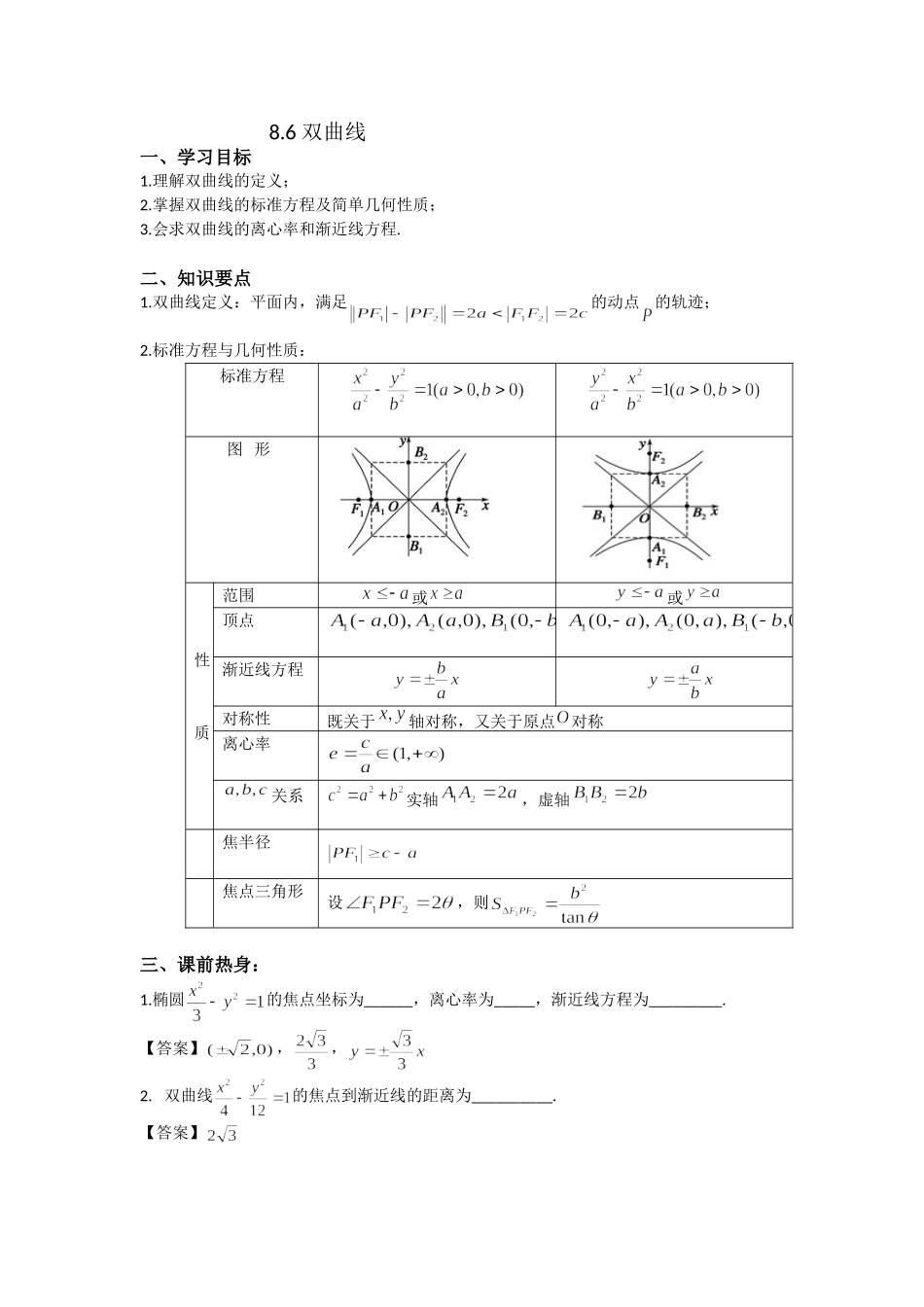
8.6双曲线一、学习目标1.理解双曲线的定义;2.掌握双曲线的标准方程及简单几何性质;3.会求双曲线的离心率和渐近线方程.二、知识要点1.双曲线定义:平面内,满足的动点的轨迹;2.标准方程与几何性质:标准方程图形性质范围或或顶点渐近线方程对称性既关于轴对称,又关于原点对称离心率关系实轴,虚轴焦半径焦点三角形设,则三、课前热身:1.椭圆的焦点坐标为______,离心率为_____,渐近线方程为_________.【答案】,,2.双曲线的焦点到渐近线的距离为__________.【答案】3.已知方程表示双曲线,则的取值范围是________.【答案】4.设是双曲线的焦点,是双曲线上一点,,则______.【答案】5.已知,,动点,则点的轨迹方程是__________.【答案】()三、典例分析例1.(1)一动圆与两圆和都外切,则动圆圆心轨迹为()A.圆B.椭圆C.双曲线的一支D.抛物线(2)已知是双曲线的左焦点,,是双曲线右支上的动点,则的最小值为.【答案】(1)C;(2)9.例2.(1)与椭圆有公共焦点,且离心率为的双曲线方程是__________.(2)已知双曲线的渐近线方程为,且过点,则该双曲线的方程为____________.【答案】(1);(2).例3.(1)设分别为双曲线的左、右焦点.若在双曲线右支上存在点,满足,且到直线的距离等于双曲线的实轴长,则该双曲线的渐近线方程为A.B.C.D.(2)已知双曲线的左焦点,其中满足,且,直线与双曲线在第二象限交于点,若(为坐标原点),则该双曲线的渐近线方程为()A.B.C.D.【答案】(1)C;(2)C.例4.(1)已知椭圆和双曲线有相同的焦点,它们的离心率分别为,是它们的一个公共点,且.若,则()A.B.C.D.(2)如图、是椭圆与双曲线的公共焦点,、分别是、在第二、四象限的公共点,若四边形为矩形,则的离心率是________.【答案】(1)B;(2).五、课外作业基础题:1.双曲线左、右焦点坐标分别是()A.,B.,C.,D.,【答案】B2.双曲线的渐近线方程为()A.B.C.D.【答案】C3.已知双曲线的右焦点为,渐近线方程为,则该双曲线实轴长为()A.2B.1C.D.【答案】A4.已知定点,动点Q在圆O:上,PQ的垂直平分线交直线OQ于M点,若动点M的轨迹是双曲线,则m的值可以是()A.2B.3C.4D.5【答案】D5.已知为双曲线(a>0,b>0)的左焦点,A为双曲线的右顶点,B(0,-b),P为双曲线左支上的动点,若四边形FBAP为平行四边形,则双曲线的离心率为()A.B.C.D.【答案】B6.已知是双曲线的右焦点,直线经...